ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 Calcul
aléatoire
d'une intégrale et du nombre
π |
Avec l'aide de
l'ordinateur et d'un petit programme en JavaScript,
nous allons calculer une aire par une méthode aléatoire (dite
de Monte-Carlo)
sans recours au calcul intégral. Notre outil sera
la loi
faible des grands nombres de
Jakob
Bernoulli.
La méthode est appliquée au :
| Théorie : |
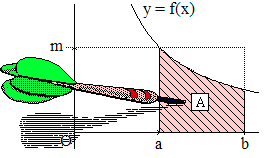
Soit f une fonction continue et positive sur [a,b] dont nous notons m le maximum sur cet intervalle. L'aire cherchée est :
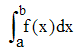
ici représentée comme une cible, est touchée par une fléchette si les coordonnées x et y de la pointe de celle-ci vérifient :
Tirons donc une fléchette en décidant que l'univers des éventualités est l'ensemble des points du rectangle délimité par les droites [x = a], [x = b], l'axe des abscisses x'x et la droite [y = m] où m est le plus grand des deux nombres f(a) et f(b). Notons S l'aire de ce rectangle. L'ordinateur va simuler le lancement d'une fléchette dans ce rectangle grâce à sa fonction génératrice de nombres aléatoires. Si cette fonction est efficace, on peut admettre l'équiprobabilité des éventualités.
La probabilité de "tomber" dans la cible, c'est à dire d'atteindre un point de l'aire A cherchée, est (intuitivement?) A/S. La répétition de N tirages engendre une variable aléatoire binomiale B(N;A/S) et, d'après la loi faible des grands nombres de Jakob Bernoulli, si on note F le nombre de fois où la fléchette est tombée dans la cible, on a donc, pour N suffisamment grand :
| Testons maintenant la méthode pour calculer le logarithme népérien de 2 : |
La fléchette est tombée dans l'aire hachurée A si son ordonnée, notée yr dans le programme, est inférieure à y = f(x), c'est à dire si yr ≤ 1/x.
i La fonction Math.random génère un nombre aléatoire. En fait le nombre u obtenu est pseudo-aléatoire : il s'agit d'une suite de nombres décimaux générés entre 0 et 1 par une récurrence du type :
où uo, a et b sont puisés, par exemple, à partir de l'heure à laquelle l'utilisateur met en route le programme. L'instruction FRAC retourne la partie décimale d'un nombre : FRAC(x) = x - E(x), c'est à dire x privé de sa partie entière.
En posant d = b - a, l'instruction x = a + d*random() fournit x dans l'intervalle ]a,b[ puisque 0 < random() < 1. Ici x variera donc de 1 à 2 : notons que le fait "d'intégrer" sur l'ouvert ]1,2[ ne modifie pas la valeur de l'intégrale. L'instruction
évite de préciser Math. devant chaque fonction mathématique utilisée.
| Programmation JavaScript de la méthode : |
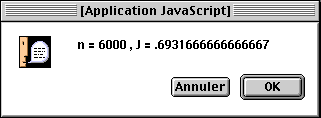
Par défaut, le programme calcule ln 2 en intégrant 1/x sur l'intervalle [1,2]. La convergence... aléatoire, est due à l'aspect non purement aléatoire de la fonction random : il n'y a pas équiprobabilité.
Le programme accepte pi (pour π) et e, base des logarithmes népériens. On peut entrer, par exemple, 2*pi/3, sqrt(e) pour √e, etc.
➔
Rappel : Votre
fonction doit être
positive
sur l'intervalle [a,b] d'intégration avec
f(a) distinct
de f(b) !
|
Testons la méthode pour calculer une valeur approchée du nombre π : |
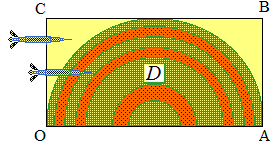On suppose, ci-dessus, A(6,0) et C(0,3). L'aire du
rectangle OABC est 18 unités d'aire; celle du demi-disque D de
diamètre OA est 9π/2.
Le rectangle OABC est la cible dans laquelle on lance des fléchettes au hasard. On admet en outre qu'aucune fléchette ne tombe en dehors du rectangle (l'ordinateur nous y aidera...)
Ici, point d'intégrale, on connaît l'aire du disque. La probabilité qu'une fléchette tombe dans le demi-cercle est égale au rapport des aires, soit :
Lançons n fléchettes et appelons F le nombre de fois où nous sommes tombés dans le demi-cercle, événement considéré comme un succès; nous sommes en présence d'une loi binomiale B(n,π/4). D'après la loi faible des grands nombres, la variable B converge en probabilité vers π/4 lorsque n tend vers l'infini. C'est dire que si n est assez grand, on doit avoir, en appelant F le nombre de fois où la fléchette est tombée dans le demi-cercle : F/n ≅ π/4, soit :
L'équation du demi-cercle est (x - 3)2 + y 2 = 9 , x variant de 0 à 6 et y, de 0 à 3.
L'ordinateur doit simuler un tirage à l'intérieur du rectangle afin que l'univers des éventualités soit effectivement les tirs dans le rectangle. Si la fléchette tombe dans le demi-cercle, F augmente de 1.
| Programmation JavaScript de la méthode : |
Cette méthode pour calculer π est bien évidemment plus insolite, voire rigolote, que précise mais "ça marche" ! Espérons que les rebelles aux stats, aux probas et à l'informatique y verront un résultat qui les convaincra... Les maths sont une et indivisible.
|
<SCRIPT LANGUAGE=JavaScript> function go() |
Aiguille de Buffon : » Autres calculs de π : »