
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Nom de la fonction : fonction exponentielle (de base e)
Notation : Exp. La notation puissance ex est due à Euler. On a l'équivalence :
C'est dire que la fonction Exp est la fonction réciproque de la fonction ln (logarithme népérien).
Etymologie de l'appellation
exponentielle : du latin exponer
= exposer : placer à côté.
Le terme est dû à Jacques
(Jakob) Bernoulli.
Ensemble de définition : R, image par réciprocité de R*+ = ]0 , +∞[ par la fonction ln (logarithme népérien).
Périodique : non.
Fonction dérivée : (ex)' = ex. Fonction primitive : x → ex
Nom de la courbe associée : pas de nom spécifique (courbe exponentielle).
Définitions possibles : celle de Jakob Bernoulli avec la condition (ex)' = ex : unique fonction coïncidant avec sa dérivée sur tout son ensemble de définition ou plus simplement, connaissant ln, compte tenu de l'équivalence déjà énoncée supra :
y = ln x ![]() x
= ey
x
= ey
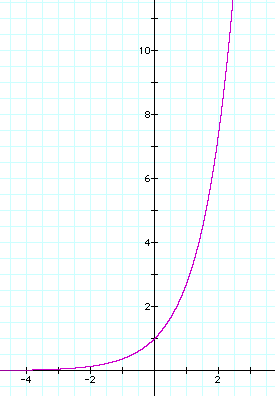
Calculs du nombre e dans ChronoMath : » Différentes approches de la fonction exponentielle : »
Limites usuelles :
|
x → -∞ |
x → +∞ |
|
|
ex |
0+ |
+∞ |
|
xex |
0- |
+∞ |
|
ex/x |
0+ |
+∞ |
|
xe-x = x/ex |
+∞ |
0+ |
∗∗∗
Appliquer une des limites ci-dessus afin de
prouver que x100000/ex tend vers 0 pour x infini
positif.
Indications : passer au log... voir aussi
par ici...
➔ On constate ci-dessous que si les courbes exponentielle et logarithmique sont tracées dans un même repère orthonormé, elles sont symétriques par rapport à la 1-ère bissectrice du repère d'équation y = x : c'est un résultat général pour deux courbes représentatives de deux fonctions réciproques l'une de l'autre.
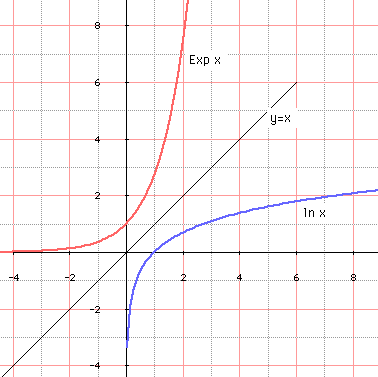
Applications :
Elles sont extrêmement nombreuses, en symbiose avec la fonction logarithmique : eu égard à l'équivalence
tout phénomène logarithmique est lié à la fonction exponentielle (et réciproquement...). Citons comme domaine privilégié de ces fonctions : l'électricité et l'électronique, la radioactivité, les statistiques et le calcul des probabilités (loi normale), la thermodynamique, les phénomènes vibratoires de type oscillatoire amorti d'équations de la forme a.e-ktcos(ωt + Φ), la cinétique des gaz, ...
| ∗∗∗ |
2. Étudier le sens de
variation de la fonction f : x
→ e2x - 2ex
+ 1. Préciser l'unique valeur de x pour laquelle f(x) = 1. On montrera que la courbe (c) représentative de f admet une asymptote horizontale (d) d'équation y = 1 au voisinage de -∞. Calculer l'aire A du domaine plan compris entre (c) et la droite (d) sur l'intervalle [-∞ , ln2]. La courbe (c) est représentée ci-dessous. Rép : A = 2 unités d'aire. |
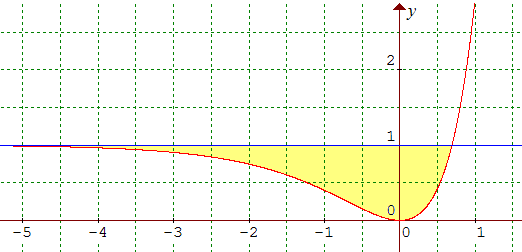
L'aire A est coloriée en
jaune. C'est la limite pour u
tendant vers -∞ de l'intégrale
sur [u , ln2] de 1- f(x) = 2ex - e2x
∗∗∗
Étude
de la fonction
f(x) = e2x - 2ex
+ 1 , asymptote, calcul d'aire
Étude d'une fonction et de sa
primitive f(x) = ln(1 + ex)/ex
et développement limité d'ordre 3
Des approches concrètes
(sciences physiques) de la fonction
exponentielle.
Lorsque le nombre a est positif, considérons les fonctions x → ax pour x réel. Le cas trivial a = 1 est proscrit. Le nombre a est appelé base : il s'agit des fonctions exponentielles de base a. Si l'on parle de la fonction exponentielle (tout court), il s'agira de la fonction x → ex, fonction exponentielle de base e.
Les logarithmes de base a, notés loga furent définis par Euler par :
y = ax ⇔ logay = x
On peut utiliser le logarithme népérien et l'exponentielle de base e pour "réexprimer" une fonction exponentielle de base a :
y = ax ⇔ ln y = x.ln a ⇔ y = ex.ln a
Par suite, les études des fonctions exponentielle et logarithme de base a ( a > 0, a distinct de 1) peuvent se déduire facilement de celles de base e et on voit donc que les fonction les fonctions x → ax sont strictement croissantes (resp. décroissantes) pour a > 1 (resp. a < 1).
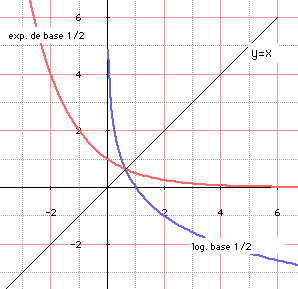
∗∗∗
Résoudre l'équation 2x+1 - 2x-1 = 3√2.
Rép. : x = 3/2
Étude d'une fonction (exponentielle de
base 2) : y = x - 2x-1
Neper, logarithmes de base a, logarithme décimal : »