ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 BERTRAND Joseph Louis
François, français,
1822-1900 |
Reçu
premier à l'École polytechnique à 17 ans, premier à l'agrégation
deux années plus tard (ex aequo avec Briot), il sera
ingénieur des Mines, fonction qu'il délaissera pour
l'enseignement au lycée Saint-Louis (Paris) puis au Collège de
France. Bertrand fut élu à l'Académie des
Sciences (1856), succédant à Sturm,
puis à l'Académie française (1884).
Bertrand publia de nombreux mémoires, en particulier dans le Journal de Liouville, et de nombreux traités comme Traité d'arithmétique (1849), Calcul différentiel et intégral, Calcul des probabilités (1889).
Plus généralement, sur le plan scientifique, ses travaux portèrent sur l'astronomie, la thermodynamique, l'électricité. Il éditera la théorie de la Lune d'Abu al-Wafa (1873). Son histoire des mathématiques sera publiée l'année de sa mort en 1900.
| Série de Bertrand : |
Pour n au moins égal à 2, il s'agit de la série de terme général :
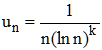
♦ Cette série converge si et seulement si k > 1
Preuve : si k < 0, un est supérieur au terme général de la série harmonique. Par conséquent, elle diverge. Si k > 0, on peut comparer la série à l'intégrale sur [2,+∞[ de f(x) = ux, x réel. Posons t = ln x, donc x = et et dx = etdt :
➔ La série de Bertrand se généralise au cas :
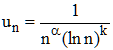
♦ Cette série est convergente ou divergente suivant que α > 1 ou α < 1.
Preuve : β désignant un réel compris entre α et 1, écrivons le terme général de la série sous la forme :
,
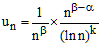Si α > 1, on a β ∈]1,α[ et la suite (un) est majorée par 1/nβ, terme général d'une série de Riemann convergente (β > 1) : le second facteur étant inférieur à 1 pour n suffisamment grand (il tend vers 0) vu que β - α < 0 et que "la puissance l'emporte sur le logarithme".
Si α < 1, on a cette fois β ∈]α,1[, donc β - α > 0, et il apparaît que le second facteur tend vers l'infini. 1/nβ,la suite (un) est donc majorée par 1/nβ, terme général d'une série de Riemann divergente (β < 1). La série considérée diverge donc.
| Paradoxe de Bertrand : |
Ce "paradoxe", qui n'en est pas vraiment un, réside dans la pluralité des solutions suivant l'interprétation que l'on peut donner de l'énoncé :
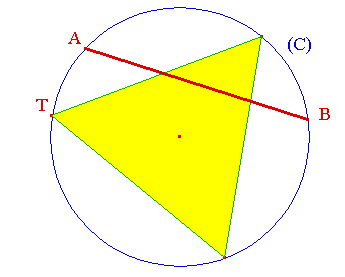
Considérons un cercle
(C) et
une corde [AB] de ce cercle tracée au hasard.
Quelle est la
probabilité que cette corde soit plus longue que le
côté du triangle équilatéral inscrit ?
La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ
) :
Vous pouvez agrandir/rétrécir le
cercle et déplacer A et B ainsi que le triangle au
moyen de T
| Postulat (conjecture) de Bertrand : |
Bertrand énonça (1845) une conjecture prouvée par Tchebychev en 1850 :
Pour tout entier naturel n au moins égal à 2, il existe un nombre premier entre n et 2n
Tchebychev prouva plus précisément :
Pour n ≥ 4, il y a au moins un nombre premier compris entre a et 2(a - 1)
Selon A. Bouvier et M. George, le mathématicien allemand Robert Breusch aurait prouvé (1931) un résultat plus éloquent :
Pour tout entier naturel n au moins égal à 48, il existe un nombre premier entre n et n + n/8 = 1,125n
Pour n = 48, on trouve 53; pour n = 55, on trouve 59 et 61, ...
» Tchebychev Étude et calculs de nombres premiers : »
➔ Pour en savoir plus :
Galton
