ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
  Trisection d'un
segment #3 niveau
4è/3è
»
#1 , #2
|
Quadrisection |
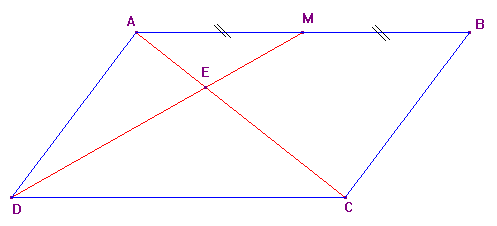
On considère un parallélogramme ABCD. On note M le milieu de [AB]. Le segment [DM] coupe la diagonale [AC] en au point E.
Montrer que AE est le tiers
de AC : AE =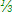 
AC
En panne ?.. Indications pour la solution : ›››› Solution (à compléter) : ››››
| Indications : |
En 4ème
En 3ème
On utilisera une configuration croisée de Thalès...
| Solution à compléter : |
En 4ème :
Soit N le milieu de DC et O le centre du parallélogramme, point de concours des diagonales.
Le .................. MBND ayant deux côtés opposés ............... et de .......... .............. est un parallélogramme.
On en déduit (DM) // (.......).
Appelons alors F le point d'intersection de [AC] avec [BN].
M étant le ............... de [AB], la r.............e de la propriété de la droite ...... .............. dans le triangle ABC, coupé par (EM) .................. (FB), permet d'affirmer que E est ............... de [........].
On a donc AE = ...........
Un raisonnement strictement identique appliqué au triangle .......... permet d'affirmer que F est le milieu de [........].
On a donc que EF = ...........
En conséquence AE = EF = FC. Par suite AE est le .......... de AC, ce qu'il fallait démontrer.
En 3ème c'est beaucoup plus simple :
La ............... de Thalès c..........ée appliquée aux droites (AM) et (........) coupées par (AC) et (DM) sécantes en ........ permet d'écrire les égalités :
EA/EC = ......./....... = AM/.......
M est le ............... de [AB] et AB = ........... Donc EA/EC = ............
C'est dire que EC est le .............. de AE et cela signifie que E est au ............ de [AC] à partir de A, ce qu'il fallait démontrer.