
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|

| Solution : |
2°/
3°/
Tu as sans doute trouvé la question, la voici :
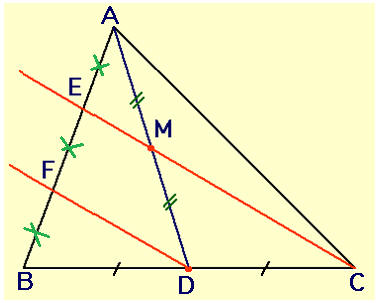
Prouver que les points E et F réalisent la trisection du segment [AB], c'est à dire :
4°/ Nous appliquons la propriété de Thalès :
AE/....... = AM/....... = 1/2 car par ................. (*), M est le ................. de [AD]
On en conclut que ...... est le ........... de [.......], donc AE = EF.
(*) ce qui est dit dans l'énoncé
On pouvait aussi appliquer la propriété de la droite des milieux :
Si une droite passe par le milieu d'un côté d'un triangle et est parallèle à un second côté, alors elle passe par le milieu du troisième côté :
Dans le triangle AFD, la droite (CM) passe par le .......... .... du côté [AD] et est parallèle à [......], elle passe donc par le ............ du côté [.....]. Par suite ..... est le milieu de [AF].
BD/....... = ......../........ = ..../....
On en conclut que ....... est le milieu de [......], donc EF = FB.
Finalement, on peut écrire AE = EF et EF = FB, donc :
AE = EF = FB = ....../3, ce qu'il fallait démontrer.