ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Résolution de triangles, cas ^a, a et b donnés     » outils Cabri

Cette figure "dynamique" illustre le cas 2.2 de l'étude que vous retrouverez en cliquant sur la clé. Sont ici donnés a = BC, b = AC et la mesure ^a de l'angle A supposé aigu :

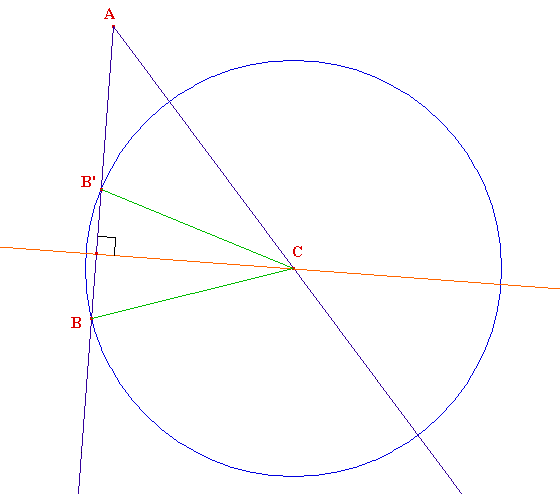
Si votre navigateur accepte les applets Java (» extension CheerpJ) :
Vous pouvez agrandir/réduire le cercle, déplacer C ainsi que les demi-droites [AB) et [AC). Déplacer A déplace toute la figure.

Afin de construire B, on trace le cercle de centre C de rayon a = BC. Par défaut, la figure présente deux solutions ABC et AB'C. Vu que CB = CB', on ^CBB' = CB'B. Par suite les angles ^ABC et ^AB'C sont supplémentaires. Autrement dit ^b = 180° - ^b'. Ce qui est conforme à la formule d'inversion du sinus : sin x = sin α  ⇔  x = α  ou  x = 180° - α.

En "tirant" C vers le bas, les points B et B' se confondent en la projection orthogonale de C sur [Ax) : cas limite dont l'unique solution est un triangle rectangle (sin^b = 1). En retournant sur la page du calcul des solutions, on comprendra mieux pourquoi la recherche de B conduit à une équation du second degré dont la solution double (Δ = 0) correspond à cos^b = 0.

 ➔  En deçà, pas de solution car b/a × sin^a = sin^b devient supérieur à 1.

• Si on pousse C vers A (a > b), on retrouve la situation ^A aigu et a > b : solution unique (cas 3.1).

• Et lorsque B' se confond avec A, on a alors CB = CA (a = b) : unique solution, triangle isocèle de sommet principal C.