
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Al-Kashi et cas élémentaires | Cas général : programme JavaScript de résolution de triangles |
➔ « Résoudre un triangle », c'est calculer la mesure de ses côtés et de ses angles. En vertu des « cas d'égalité des triangles », trois données suffisent généralement mais il y a des exceptions comme le montre cet exercice pour lequel il existe deux solutions non isométriques (non superposables).
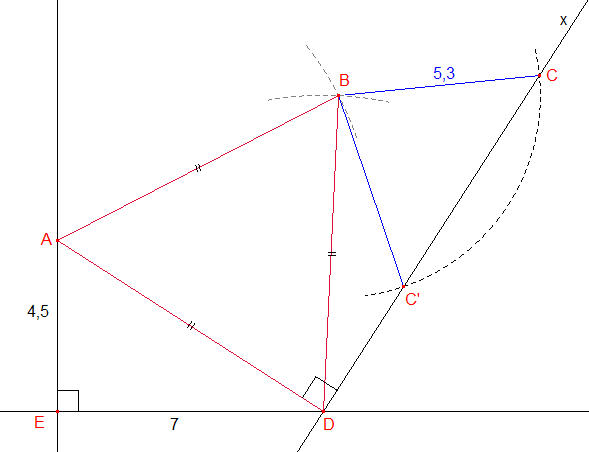
1. Construire la figure ci-dessus en respectant les codages et mesures indiqués; les arcs en pointillés indiquent le mode de construction :
On construit tout d'abord le triangle rectangle AED, puis le triangle équilatéral ABD;
On trace la droite (Dx) perpendiculaire à [AD] passant par D;
On constate que l'on peut placer sur (Dx) deux points C et C' à 5,3 cm de B.
1. Résoudre les triangles AED et ABD sans utiliser le programme en ligne ! On donnera les réponses en cm et degrés décimaux en arrondissant au millième. Les calculs successifs pourront utiliser les valeurs arrondies.
2. Résoudre le triangles DBC, DBC' et BCC'.
3. Facultatif : Vous pouvez vérifier au moyen du programme en ligne (ou simplement au moyen du rapporteur et du double décimètre ) le bien-fondé de vos calculs.
➔ On rappelle la formule d'Al-Kashi a2 = b2 + c2 - 2bc.cos et la formule des sinus dans le triangle plan, souvent attribuée à Al-Kashi mais dont la paternité revient à Al-Biruni :
![]()
Si vous séchez après avoir bien cherché : ››››
| Solution : |
! La consigne de l'énoncé autorisant l'usage des valeurs arrondies dans les calculs successifs, on usera parfois ci-après du signe d'égalité (=) au lieu, en toute rigueur, du signe d'égalité approchée (≃).
1. Triangle rectangle AED :
L'application du théorème de Pythagore fournit AD = √(AE2 + ED2) = √69,25 = 8,3216... ≃ 8,322.
tan^EAD = 7/4.5, d'où ^EAD = 57,2647... ≃ 57,265 (en degrés décimaux; arrondi au millième).
^EDA = 90 - ^EAD ≃ 32,735.
AE = 4,5 cm , ED = 7 cm , AD ≃ 8,322 cm | ^E = 90° , ^A ≃ 57,265° , ^D ≃ 32,735°
Triangle ABD :
Ce triangle est équilatéral, donc AB = AD = BD = 8,322 cm; ses angles mesurent 60°.

2. Triangle DBC :
^BDC = 90° - 60° = 30°.
Dans le triangle DBC, la formule d'Al-Biruni permet d'écrire BC/sin^BDC = BD/sin^BCD, soit 5,3/0,5 = 8,322/sin^BCD; on en déduit : sin^BCD = 8,322/10,6; d'où ^BCD = 51,7294... ≃ 51,729 (en degrés décimaux).
Il s'ensuit : ^DBC = 180° - (30° + ^BCD) ≃ 98,271.
Calculons DC : on a DC/sin^DBC = BC/sin^BDC,
soit DC/sin![]() 98,271
= 5,3/0,5.
98,271
= 5,3/0,5.
d'où DC = 10,6 × sin![]() 98,271
= 10,4897... ≃ 10,490.
98,271
= 10,4897... ≃ 10,490.
BC = 5,3 cm , BD ≃ 8,322 cm , DC ≃ 10,490 cm | ^BDC = 30° , ^DBC ≃ 98,271° , ^BCD ≃ 51,729°
3. Triangle BCC' :
Par construction, ce triangle est isocèle : BC = BC' = 5,3.
^BCC' = ^BC'C = ^BCD
≃ 51,729.
Par suite, ^CBC'
≃ 180° - 2 × 51,729° ≃ 76,542°.
Pour le calcul de CC', on peut utiliser
indifféremment les formules d'Al-Kash
ou d'Al-Biruni; choisissons la
première citée : CC'2 = BC2 + BC'2 -
2BC.BC'.cos^CBC', soit : CC' = √[2 × 5,32(1 - cos![]() 76,542)];
ce qui conduit à CC'
≃ 6.565.
76,542)];
ce qui conduit à CC'
≃ 6.565.
➔ L'usage de la formule d'Al-Kashi s'avère peu pratique si elle conduit à une équation du second degré. On pourra s'en persuader en étudiant la solution donnée en cet exercice similaire.
BC = BC' = 5,3 cm , CC' ≃ 6,565 cm | ^BCC' = ^BC'C ≃ 51,729° , ^CBC' ≃ 76,542°
4. Triangle DBC' :
^BDC' = 30°, ^BC'D = 180° - ^BC'C ≃ 128,271°.
^DBC' = ^DBC - ^CBC' ≃ 98,271 - 76,542 ≃ 21,729
Par construction, BC' = BC = 5,3. DC' = DC - CC' ≃ 10,490 - 6,565 ≃ 3,925.
BD ≃ 8,322 cm , BC' = 5,3 cm , DC' ≃ 3,925 cm | ^BDC' = 30° , ^BC'D ≃ 128,271° , ^DBC' ≃ 21,729°