ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Une application des rotations #3         niveau 3ème/2nde        » #1 , #2 , #3bis , #4 , #5 , #6

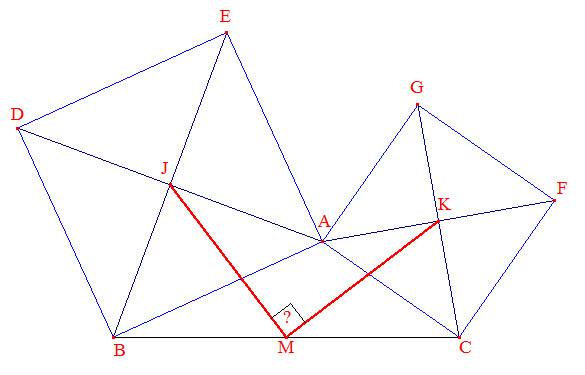
Ce petit problème n'est autre qu'un cas particulier du théorème de van Aubel : on considère un triangle ABC sur lequel on construit les carrés extérieurs ABDE et ACFG comme indiqués, de centres respectifs J et K. Soit M le milieu de [BC].

On demande de prouver que les segments [MJ] et [MK] sont perpendiculaires.

Si ton navigateur accepte les applets Java (utilise CheerpJ) :
Tu peux déplacer A, B et C

Indications pour la solution :

Tracer [CE] et [BG] : voyez figure ci-dessous.

a/ 

• Justifier (MJ) // (CE);

• Justifier (MK) // BG;

• Justifier MJ = CE/2 et MK = BG/2.

b/ 

• Justifier que la rotation de centre A, d'angle 90° transforme B en E.

• En déduire (BG) ⊥ (CE) et BG = CE.

»  Cette étape correspond à la variante  #2

c/ 

• Conclure en utilisant a/.