ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 Une
application élémentaire des rotations #6
niveau 3ème/Seconde |
Autres
cas |
 |
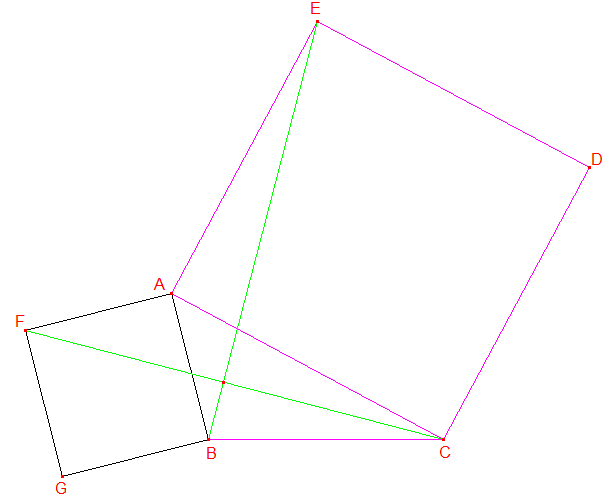
On considère un triangle ABC à partir duquel on construit extérieurement les carrés ABGF et ACDE.
1°) Montrer que les triangles AFC et ABE sont égaux (superposables).
2°) Justifier que les segments [FC] et [BE] sont perpendiculaires. Pour cela, on utilisera une rotation de centre A.
Si tu sèches après avoir bien cherché : »
| Solution : |
1°)
Considérons l'angle ^FAC du triangle AFC : sa mesure est la somme 90° + ^BAC;
Considérons maintenant l'angle ^BAE du triangle ABE : sa mesure est la somme ^BAC + 90°.
Nous avons d'autre part :
AF = AB et AC = AE.
Les triangles AFC et ABE possèdent par conséquent un angle égal compris entre deux côtés respectivement égaux (les côtés de chaque carré). Ces triangles sont donc égaux en vertu du 1er cas d'égalité des triangles.
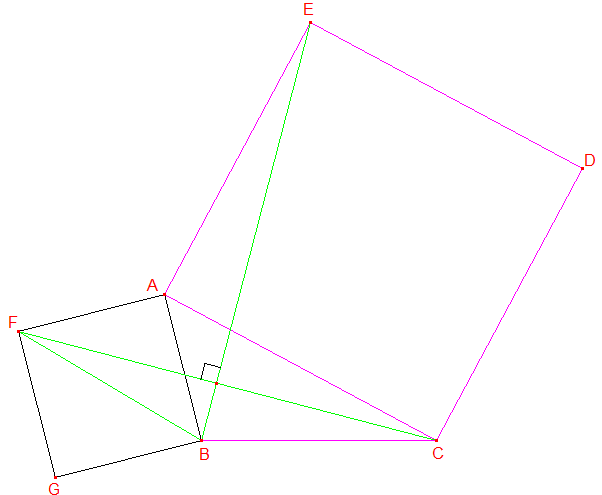
2°) La rotation de centre A d'angle 90°, dans le sens inverse des aiguilles d'une horloge transforme :
F en B et C en E;
Par suite cette rotation
transforme [FC] en [BE] : c'est dire que [FC] et [BE] sont perpendiculaires.