ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Une application des rotations #5    niveau TerS    Outil complémentaire : nombres complexes     (théorème de Van Aubel)               » Solution géométrique | Autres cas plus élémentaires

On considère un quadrilatère quelconque ABCD (en bleu ci-dessous). On construit sur ses côtés, et extérieurement, les quatre carrés de centres M, P, Q et R, points de concours de leurs diagonales respectives.

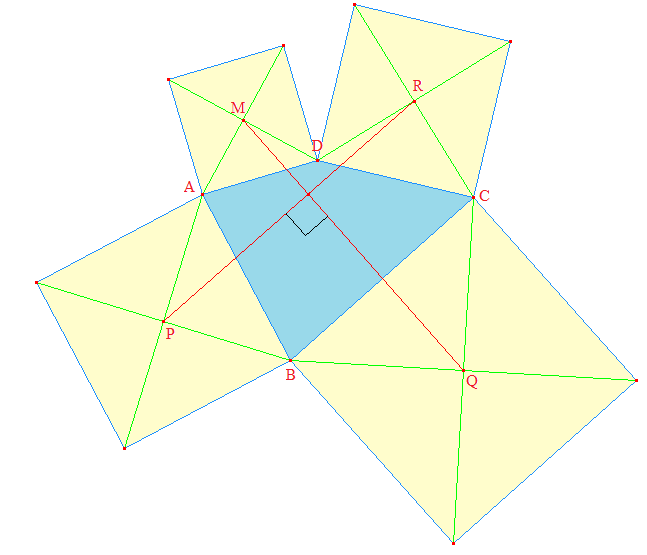
Question :      

Établir, en passant dans le plan complexe, que les segments [MQ] et [PR] sont perpendiculaires et de même mesure

Réponse :      

Considérons la figure ci-dessous où les points géométriques ont été remplacés par leurs affixes respectifs (écrtits en minuscules). Attachons-nous au carré de centre (affixe) m. Le symétrique de d par rapport à m s'obtient aussi par rotation de centre a d'angle +π/2. Si z est l'affixe de ce symétrique, on a donc :

z - a = e^iπ/2 x (d - a) = i(d - a), d'où z = a + i(d - a)

et de m = (d + z)/2, on déduit : m = ½[a + d + i(d - a)].

On calcule de même :

• p = ½[b + a + i(a - b)]
• q = ½[c + b + i(b - c)]
• r = ½[d + c + i(c - d)]

Par conséquent, par différence, nous obtenons :

• m - q = ½[a + d - c - b + i(d - a - b + c)]
• r - p = ½[d + c - b - a + i(c - d - a + b)]

Et on constate que i(r - p) = m - q : on passe donc de PR à QM par rotation d'angle π/2.
C'est dire que  (PR) ⊥ (QM) et PR = QM.

Solution purement géométrique : »