Construction d'un triangle connaissant 3 médianes

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Apprendre à construire : constructions de triangles #10
TD niveau 4è/2nde » #1 à 4 , #5 , #6 , #7 , #8 , #9

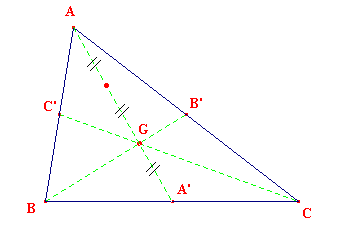
On demande de construire un triangle ABC dont on ne connaît que les mesures des trois médianes AA', BB' et CC'.

Niveau seconde : l'étude du problème devrait vous mener à énoncer une condition nécessaire et suffisante afin que cette construction soit possible.

Rappels :

Dans un triangle, les médianes sont les droites passant par un sommet et le milieu du côté opposé. En fait, on les assimile souvent à un segment (comme [AA'] ci-dessous).

Les médianes sont concourantes en un point G (centre de gravité) situé au tiers de chaque médiane à partir de leur « pied » : les pieds des médianes sont les milieux des côtés du triangle : A', B' et C'. Ce qui revient à dire aux deux tiers à partir du sommet.

Si tu sèches après avoir bien cherché : ››››

Solution :

Analyse :

Considérons un triangle ABC de centre de gravité G. Soit G' le symétrique de G par rapport au milieu A' de [BC]. Le quadrilatère BGCG' dont les diagonales ont même milieu est un parallélogramme.

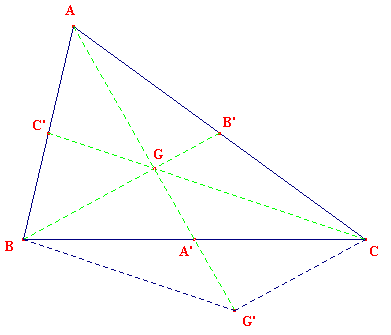
Les médianes se coupant aux 2/3 à partir de leur sommet, on a :

BG = 2BB'/3 , BG' = CG = 2CC'/3 , GG' = AG = 2AA'/3

Construction :

Un point arbitraire B étant choisi dans le plan, on construit le triangle BGG' au moyen des mesures ci-dessus. On note ensuite A' le milieu de [GG']. Le côté [BC] est obtenu avec C symétrique de B par rapport à A'. Le sommet A sera obtenu par symétrie de G' par rapport à G.

On voit que la construction sera possible si et seulement si l'inégalité triangulaire est vérifiée pour la construction de BGG', soit :

| BG - GG' | < BG' < BG + GG'

C'est à dire, au moyen des données (les médianes) :

| BB' - AA' | < CC' < BB' + AA'

Synthèse :

Bien que cela paraisse évident, voire superfétatoire..., nous devons maintenant vérifier que le triangle ainsi construit vérifie les conditions de l'énoncé.

➔ Toute construction doit être conduite par analyse et synthèse. L'analyse est le raisonnement aboutissant à la construction cherchée. Mais le processus d'analyse procède par implication : si ABC existe (on suppose la construction aboutie) alors on a nécessairement (forcément en langage élève) ceci ou cela, donc on va faire ceci ou cela.

La synthèse consiste à vérifier que ces conditions nécessaires aboutissant à la construction sont aussi suffisantes, c'est à dire que cette construction vérifie bien toutes les hypothèses de l'énoncé.

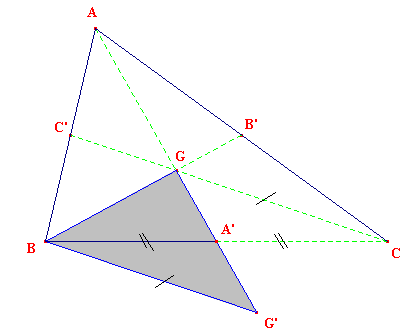
Notons x, y et z les mesures des médianes données initialement, à savoir AA' = x, BB' = y, CC' = z.

Ayant construit BGG' puis A et C comme indiqué, BGCG' est, par construction, un parallélogramme, A' est le milieu de [BC] et de [GG'], G est celui de [AG']. Par conséquent AG mesure 2x/3 : c'est dire que G est le centre de gravité du triangle ABC dont la médiane AA' mesure x.

(CG) coupe [AB] en C' et (BG) coupe [AC] en B'. On obtient ainsi les médianes (BB') et (CC'). BGCG' étant un parallélogramme, on a CG = BG' = 2y/3. De même BG = 2z/3 : on a donc bien BB' = y et CC' = z.