ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Étude d'une courbe paramétrée #2     » #1 ,#3       » coordonnées paramétriques

On se propose ici d'étudier et de tracer, dans un repère orthonormé d'unité 3 cm, la courbe G définie paramétriquement par :  

x = f(t) = e^sinpt , y = g(t) = e^cospt , t réel

1°) Prouver que la courbe G :

a) est fermée et décrite entièrement pour t∈[0,2].

b) possède deux points situés sur la bissectrice principale du repère (d'équation y = x).

c) est symétrique par rapport à la bissectrice principale du repère (d'équation y = x).

d) n'admet pas de point double.

2°) Étudier les variations de x et de y pour t variant de 0 à 2. En déduire l'allure de la courbe G. Faire apparaître le sens de parcours et la partie de G correspondant à t variant de 1/4 à 5/4.

1°)  a/ Les fonctions f et g ont pour période 2p/p = 2. Donc f(t) = f(t + 2) et g(t) = g(t) + 2. La courbe G est donc décrite entièrement pour t variant de 0 à 2.

b/ Les points de G situés sur [y = x] vérifient sinpt = cospt, t∈[0,2] et sinpt = cospt ⇔ sinpt = sin(p/2 - pt), ce qui fournit t = 1/4 + k, k entier. Les seules possibilités sont alors t = 1/4 et t = 5/4, soit :

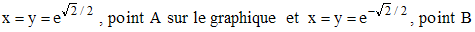
c/ La transformation X = y = e^cospt , Y = x = e^sinpt, symétrie d'axe la droite [y = x], laisse G invariante. En effet, en posant u = ½ - t, on obtient X = e^cospt = e^{cosp(½ - u)} = e^{cos(p½ - pu)} = e^sinpu et Y = e^cospu, u variant de -3/2 à 1/2, d'amplitude 2 (période de la courbe).

d/ Si G admet un point double, on a nécessairement l'égalité des abscisses : e^sinpt = e^sinpt' avec t - t' ≠ 2k, k entier. Ce qui conduit pt = pt' [2k],  ou pt = p - pt' [2k]. Le 1er cas est à rejeter. Le second fournit t = 1 - t' [2k] et, en reportant dans les ordonnées, on devrait avoir : cospt = cospt', ce qui est faux car cosp(1 - t') = cos(p - pt') = - cospt'. G n'admet donc aucun point double.

2°) f et g sont dérivables, f '(t) = pcospt.e^sinpt est du signe de cospt. g'(t) = -psinpt.e^cospt est du signe de -sinpt. On dresse sans difficultés le tableau des variations de x et de y :

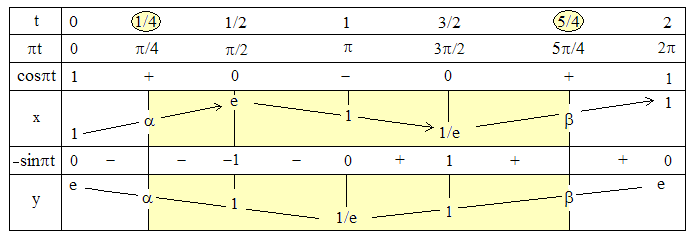
• f(1/4) = g(1/4) = exp(√2/2) = a ≅ 2,028; f '(1/4) = -g'(1/4) : tangente en (a,a) perpendiculaire à [y = x].

• f(5/4) = g(5/4) = exp(-√2/2) = b ≅ 0,493; f '(5/4) = -g'(5/4) : tangente en (b,b) perpendiculaire à [y = x].

Lorsque t varie de 1/4 à 5/4, on obtient la partie de G (en bleu ci-dessous) partant du point A(a,a) aboutissant au point B(b,b)

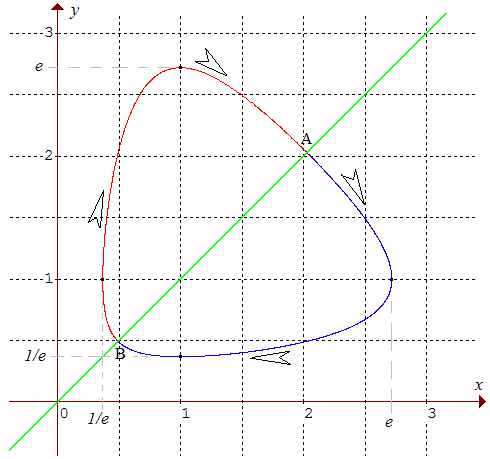
• f(1/2) = e, g(1/2) = 1; f '(1/2) = 0,  g'(1/2) = 1 : tangente "verticale" en (e,1). De même en (1/e,1) lorsque t = 3/2.

• f(1) = 1, g(1) = 1/e; f '(1) = -p,  g'(1) = 0 : tangente "horizontale" en (1,1/e). De même en (1,e) lorsque t = 0.