ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Étude d'une courbe paramétrée du plan
niveau Suprebroussement de 1ère espèce, asymptote horizontale et point double |
Dans le plan euclidien rapporté à un repère orthonormé d'origine O, on considère la courbe paramétrée (C) définie par :
x = 2t - 1/t2 , y = 2t + t2, t décrivant R*
1°/ En étudiant les sens de variation de x et y, représenter la courbe (C) en choisissant 2cm comme unité. Prouver l'existence d'une asymptote horizontale à la courbe.
2°/ Vérifier que le point A(-3,-1) est un point de rebroussement de 1ère espèce.
3°/ Monter que la courbe (C) admet un point double D dont on calculera les coordonnées..
Si vous séchez après avoir bien cherché :
››››
1°/ x'(t) = 2 + 2/t3 = 2(t3 + 1)/t3 et y' = 2 + 2t = 2(t + 1). On établit sans difficulté le tableau de variation de x(t) et y(t) :
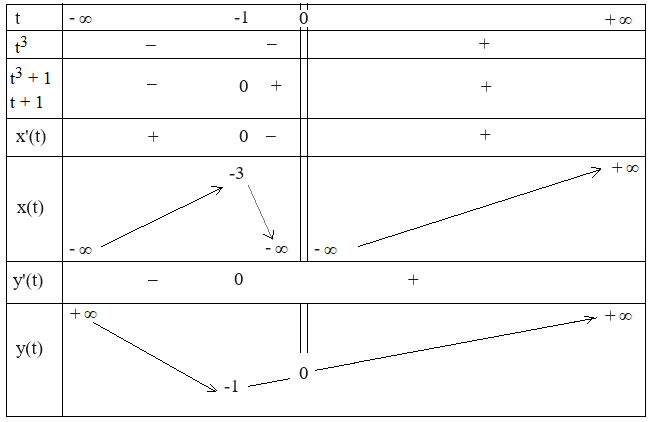
Pour t infini, x et y sont infinis et le rapport y/x est en t/2 : il s'agit donc de branches paraboliques.
Lorsque t tend vers 0 : x tend vers - ∞ et y tend vers 0 : (C) admet le demi-axe des abscisses négatives comme asymptote horizontale.
2°/ x'(t) et y'(t) s'annulent en t = -1. Le point A(-3,-1) est un point stationnaire. x"(t) = -6/t4 et y"(t) = 2. On a donc T2(-6,2) non nul en t = -1. Ce vecteur dirige la tangente en A. x'''(t) = 24/t5, y'''(t) = 0 : en t = -1, T3(24/t5,0) a pour coordonnées (24,0); ce vecteur est linéairement indépendant de T2. En accord avec la théorie des points stationnaires, p = 2 pair , q = 3 impair : il s'agit donc en A d'un point de rebroussement de 1ère espèce dont l'équation de la tangente est x + 3y + 6 = 0 (en vert sur le graphique, en écrivant que pour tout M(x,y) de cette droite, le vecteur AM est colinéaire à T2).
3°/ Recherche des points doubles : il s'agit de rechercher deux valeurs distinctes a et b du paramètre t conduisant aux mêmes valeurs de x et de y :
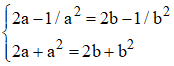
Ce système conduit facilement à a + b = -2 et ab = ±1. On utilise l'équation classique X2 - SX + P = 0 où S représente a + b et P le produit ab :
Si ab = 1, il résulte que (X + 1)2
= 0, donc a = b = -1, à rejeter car a doit être distinct de b.
On remarquera
que cela correspond au point de rebroussement A(-3,-1).
Si ab = -1, il résulte que X2
+ 2X - 1= 0, donc t = - 1 ± √2.
Ces deux valeurs du paramètre t conduisent à
(x,y) = (-5,1), point D.
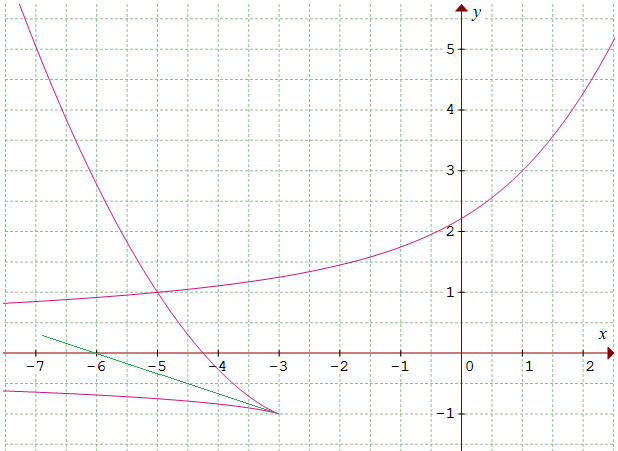
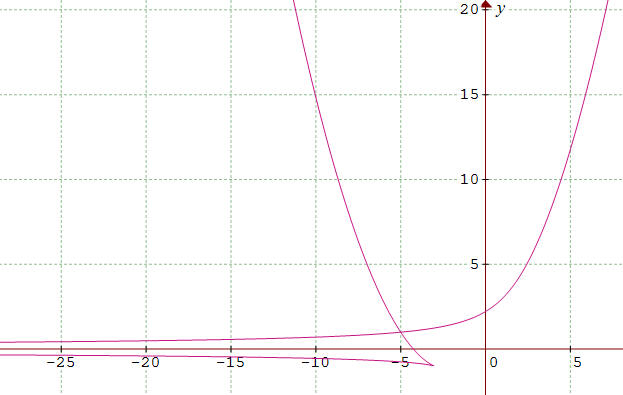
En "reculant", on voit mieux
apparaître l'asymptote horizontale pour t tendant vers 0