ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Étude d'une courbe paramétrée #1      »   #2 , #3    » coordonnées paramétriques

On étudie ici la courbe Γ définie par :

x = f(t) = sint.cos2t , y = g(t) = cost , t réel.

•  Les fonctions définissant x et y sont 2π-périodiques, la courbe sera donc obtenue entièrement en restreignant t à l'intervalle [0,2π].

•  f(-t) = -f(t) et g(-t) = g(t) : la courbe Γ admet Oy comme axe de symétrie; on peut donc réduire l'intervalle d'étude à [0,π] et compléter par symétrie / Oy.

•  f(π - t) = f(t) et g(π - t) = -g(t) : la courbe Γ admet également Ox comme axe de symétrie.

 ➔    On peut donc réduire l'intervalle d'étude à [0,π/2] et compléter par symétrie / Ox puis par rapport à Oy :

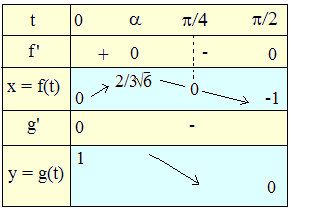
•  f et g sont dérivables et on vérifiera que f '(t) = cost(1 + √6sint)(1 - √6sint).

Sur l'intervalle d'étude [0,π/2], f ' garde le signe de 1 - √6sint et s'annule en α tel que sinα = 1/√6, ainsi qu'en π/2.
Concernant y, g'(t) = -sint reste négative (nulle en 0) sur l'intervalle d'étude :

On obtient une fort jolie courbe : l'arc rouge correspond à l'intervalle [0,π/2]; on a complété par symétrie / Ox suivie d'une symétrie /Oy. Les fléchettes indiquent le sens de parcours depuis le point de coordonnées (0;1) correspondant à t = 0.

 ➔  On remarque la présence de deux points doubles dont la recherche n'est pas toujours simple. Dans ce cas paramétré où x et y sont des fonctions trigonométriques de t, un point M sera double (voire multiple) s'il correspond à des valeurs distinctes de t dont la différence n'est pas un multiple de la période.

Au vu du graphique, il est clair qu'ils correspondent à t = π/4 et t = 7π/4 d'une part et à t = 3π/4 et t = 5π/4 d'autre part. Montrons-le : il s'agit de rechercher des points M correspondant à des valeurs distinctes a et b de t avec b distinct de a + 2kπ :

sin a.cos2a = sin b.cos2b , cos a = cos b  , b ≠ a + 2kπ

la seconde équation, cos a = cos b, équivaut à a = b + 2kπ (à rejeter) ou a = - b + 2kπ; c'est dire que a = 2π - b. On remplace dans la première équation, il vient sinb.cos2b = 0, or :

sinb.cos2b = 0 ⇔ b = kπ ou b = ±π/4 + kπ.

On vérifie facilement alors que seuls les paires {a,b} = {π/4,7π/4} et {a,b} = {3π/4,5π/4} conviennent.