ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
TONELLI Leonida,
italien, 1885-1946 |
Après des études supérieures de mathématiques à l'université de
Bologne où Pincherle et
Arzela (qui dirigea sa thèse, 1906) furent ses professeurs, Tonelli se consacra
comme ses maîtres à l'analyse à travers le calcul des variations (Fondamenti
di calculo delle variazioni, 1921) et la théorie
moderne de l'intégration (dans le cadre de la théorie de la mesure initiée par
Lebesgue), à l'instar
de ses ainés et compatriotes Fubini et
Volterra.
Il enseigna principalement à Parme (1914-1922), à Bologne (1922-1930) et à l'École normale supérieure de Pise de 1930 jusqu'à sa mort.
» Sources : portrait et extraits biographiques → SISM (Società Italiana di Storia delle Matematiche)
L'important théorème d'intégration sous le signe ∫ sur un pavé borné de R2, attribué généralement à Fubini, doit être, en toute équité également alloué à Tonelli ! On peut ainsi l'énoncer :
|
Théorème de Fubini-Tonelli : |
U désigne un pavé de R2 défini par a ≤ x ≤ b , c ≤ y ≤ d, une borne au moins étant infini; f est une fonction numérique des deux variables x et y. Si f est intégrable sur U, alors les intégrales simples (éventuellement généralisées) présentes dans les égalités ci-dessous existent et :
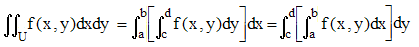
➔ Si (x,y) → f(x,y) n'est pas déclarée intégrable, l'existence des deux dernières intégrales n'est pas assurée. Tonelli précise alors dans le cadre plus général de l'intégrale de Lebesgue :
Si (x,y) → f(x,y) est mesurable et positive sur U, l'existence d'un des trois membres de l'égalité ci-dessus implique l'existence des deux autres (et par suite l'égalité des trois membres qui ont alors un sens).
» Fubini
➔ Pour en savoir plus :
Weyl