ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

SIMSON Robert, écossais, 1687-1768

 !    On ne le confondra pas avec l'algébriste Thomas Simpson.

Géomètre, professeur de mathématiques à l'université de Glasgow de 1711 à 1762. Les travaux de Simson portent sur les coniques (1735) où il développe les résultats obtenus par Desargues, précurseur de la géométrie projective.

Simson s'adonna à des recherches sur l'œuvre d'Euclide dont il traduisit les éléments en anglais (1756). Son nom reste attaché à une droite particulière du triangle :

Théorème et droite de Simson :   

Une condition nécessaire et suffisante pour que les projetés orthogonaux J, K et L d'un point M du plan sur les supports des côtés d'un triangle ABC soient alignés sur une droite (d) est que M appartienne au cercle circonscrit à ABC.

La droite (d) est la droite de Simson du point M relativement au triangle ABC

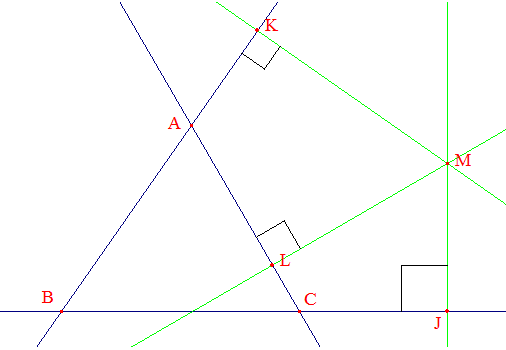
Preuve : J, K et L sont alignés si et seulement si  ^(JM,JL) = ^(JM,JK) : égalité d'angles de droites (modulo π). On a ^MJC = ^MLC = 90°, par conséquent les points M, J, C et L sont cocycliques et on peut alors écrire : ^(JM,JL) = ^(CM,CL). On a de même, en considérant le quadrilatère BKMJ :  ^(JM,JK) = ^(BM,BK).  Notre condition d'alignement peut s'écrire maintenant :  ^(BM,BK) = ^(CM,CL) ou encore  ^(BM,BA) =  ^(CM,CA) : cette égalité équivaut à la cocyclicité des quatre points ABCM : M appartient au cercle circonscrit au triangle ABC.

Si votre navigateur accepte les applets Java  (» extension CheerpJ) :
Vous pouvez déplacer le point M : J sera sur (KL) si et seulement si M est sur le cercle circonscrit au triangle ABC.

Elle exprime une relation de récurrence entre trois termes consécutifs de la célèbre suite de Fibonacci :

---

Bernoulli Nicolas Ier  Goldbach

---

© Serge Mehl - www.chronomath.com