ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 BINET Jacques
Philippe Marie,
français, 1786-1856 |
Polytechnicien
(1804), ingénieur des Ponts et chaussées, Binet fut professeur de mécanique à
l'École polytechnique, succédant à Poisson en 1815. Il obtint une chaire
d'Astronomie au Collège de France (1823). Royaliste et engagé politiquement,
Binet devra renoncer à son poste de directeur des études à l'École polytechnique
lors de la chute de Charles X (révolution de 1830).
Binet publia un grand nombre de mémoires portant sur la mécanique et l'astronomie. Ses travaux mathématiques portent, en algèbre linéaire, sur la théorie des déterminants initiée par Cauchy où il apparaît comme pionnier dans ce qu'on appellera, avec Cayley, le calcul matriciel.
Son nom est resté attaché à la formule portant son nom (ci-dessous) et, en mécanique rationnelle, à des formules précisant les vitesse et accélération d'un mobile soumis à une accélération centrale. Il collabora à une nouvelle édition de la Mécanique céleste de Lagrange (1816). Binet fut élu à l'Académie des sciences en 1843 succédant à Lacroix.
| Formule de Binet pour la suite de Fibonacci (1843) : |
Cette très belle formule, que connaissait cependant de Moivre, fournit le n-ème nombre de la célèbre suite des entiers de Fibonacci uo = u1 = 1 :
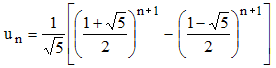
Avec la notation Φ = (1 + √5)/2 (nombre d'or), on a (√5 - 1)/2 = 1/Φ (section dorée), on peut écrire de façon plus pratique et condensée :
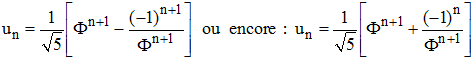
Preuve de la formule : »
Horner