ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
De GUA de MALVES Jean-Paul,
français, 1712-1786 |
Prêtre, philosophe et mathématicien, l'abbé de Gua (parfois du Gua), admirateur de Descartes, fut professeur de philosophie au collège de France et publia (1740) un traité sur les courbes intitulé : Usage de l'analyse de Descartes pour découvrir, sans le secours du calcul différentiel, les propriétés des lignes géométriques de tous les ordres.
Dans ce travail, il achevait en particulier la classification des courbes algébriques du 3ème degré (cubiques) entamée par Newton et déjà complétée par Stirling (1717). A ce sujet, on lui doit la première preuve du résultat selon lequel :
Si une cubique admet trois points d'inflexion, alors ces trois points sont alignés
D'Alembert lui rend souvent hommage dans son Encyclopédie : De Gua lui-même projetait la mise en œuvre d'une encyclopédie universelle, ce projet aurait inspiré d'Alembert. Il fut élu à l'Académie des sciences en 1741 : cette année-là il publiait un important mémoire sur la résolution des équations algébriques prenant en compte toutes les solutions réelles ou non (» réf. 2).
Points singuliers d'une courbe, inflexion : »
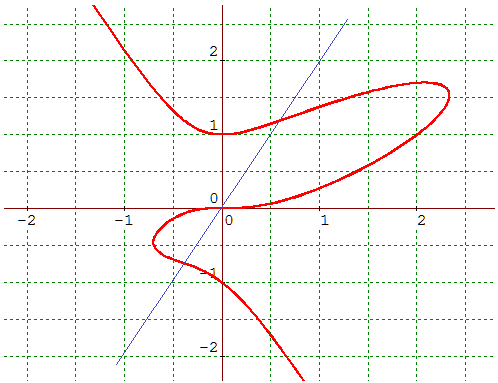
x3
+ y3 - 2yx2
+ xy2 - xy - y =
0, trois points d'inflexion alignés
Un lecteur passionné et courageux
pourra se lancer dans la recherche de ces trois points d'inflexion en utilisant
le théorème des fonctions implicites...
Coniques selon d'Alembert : » Racine d'une équation selon d'Alembert : »
➔ Pour en savoir plus :
Éloge de l'abbé de Gua de Malves, Histoire de
l'Académie royale des sciences, pages 75 de la pagination BnF :
http://gallica.bnf.fr/ark:/12148/bpt6k3585j.image.swf
Recherche du nombre des racines réelles et imaginaires, réelles positives ou réelles négatives qui peuvent se trouver dans les équations de tous les degrés par M. l'abbé de Gua : http://gallica.bnf.fr/ark:/12148/bpt6k5504414v/f683.image.r=de Gua.langFR
Le rang des courbes de Mordell (CNRS, Images des mathématiques) et l'étude du groupe des points à coordonnées rationnelles : http://images.math.cnrs.fr/Le-rang-des-courbes-elliptiques.html
König