ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
KOEBE Paul,
allemand, 1882-1945 |
Paul Koebe étudia les mathématiques à l'université de Berlin. Il obtint son doctorat (1905) sous la direction de Hermann Schwarz sur un sujet portant sur les fonctions analytiques d'une variable complexe.
Poursuivant ses études à Göttingen, il résout (über die Uniformisierung der algebraischen Kurven, 1907), âgé de 25 ans, indépendamment de Henri Poincaré (quelques mois plus tard), le difficile 23è problème de Hilbert relatif à l'uniformisation des fonctions analytiques complexes au moyen de fonctions automorphes (fonctions fuchsiennes). Koebe fut principalement professeur à Iéna et à Leipzig.
Fonctions de Koebe :
Il s'agit des fonctions d'une variable complexe :
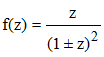
Ces fonctions sont holomorphes sur le disque ouvert unité |z| < 1 et admettent le développement en série entière :
z/(1 + εz)2 = Σnεnzn (n ≥ 1, ε = ±1)
Elles jouent un rôle important dans le problème uniformisation des fonctions analytiques injectives (fonctions schlicht) et dans la preuve de la conjecture de Bieberbach :
Toute fonction holomorphe φ injective sur le disque unité |z| < 1 telles que φ(0) = 0 et φ'(0) = 1 vérifient les inégalités de distorsion :
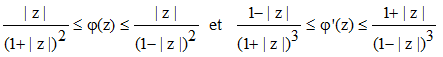
Les égalités n'ayant lieu que si φ est une fonction de Koebe.
➔ Pour en savoir plus :
Moore
Robert Lee