
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Fils d'un médecin hollandais expatrié en 1870, Birkhoff fit ses études à Chicago. Brillant étudiant, il entre à l'université de Harvard en 1903 mais reviendra soutenir sa thèse de doctorat (1907) à Chicago, sous la direction de E. H. Moore, portant sur les "propriétés asymptotiques de certaines équations différentielles" (Asymptotic Properties of Certain Ordinary Differential Equations with Applications to Boundary Value and Expansion Problems).
Après les universités du Wisconin et de Princeton, Birkhoff obtient un poste à Harward (1912) qu'il conserva jusqu'à sa mort en 1944. Ayant encadré un nombre considérable d'étudiants en mathématiques, on le considère comme un des plus grands mathématiciens américains de la première moitié du 20è siècle. Il fut à Harvard un collègue et ami de Saunders Mac Lane avec lequel il écrivit trois traités d'algèbre moderne.
Son champ de recherche, très large, dans le prolongement des travaux de Poincaré, porta sur l'analyse où il introduit le calcul matriciel dans la résolution des systèmes différentiels et des équations aux différences, les séries semi-convergentes (appelées asymptotiques par Poincaré), les bases mathématiques de la théorie de la relativité et la mécanique quantique, la mécanique céleste (la preuve, en 1913, d'un résultat énoncé par Poincaré, voir ci-après, assoit sa réputation internationale) et, tout particulièrement, en théorie des systèmes dynamiques (dès 1912) pour laquelle il établit, s'appuyant sur la toute nouvelle théorie de la mesure et l'intégrale de Lebesgue, le théorème ergodique qui porte son nom.
|
Le théorème de Poincaré-Birkhoff et le problème des trois corps : |
En 1912, lors de ses recherches en vue de résoudre le problème des trois corps, un problème de mécanique céleste newtonienne, Poincaré émit une conjecture, parfois appelé dernier théorème géométrique de Poincaré, qu'il ne démontra que partiellement. En janvier de l'année suivante, Birkhoff en présente la démonstration (publiée dans les Transactions of the American mathematical Society) :
Dans le plan orienté, soit Γ la couronne du plan de bords Cr et Cr' (cercles concentriques, r > r') et T une transformation continue et bijective laissant Γ invariant, conservant les aires et faisant avancer les points de Cr dans le sens positif et ceux de Cr' dans le sens négatif. Alors T possède au moins deux points invariants.
La preuve de Birkhoff (en français, sur le site Numdam) : »
On trouvera en fin de page (» réf.3) la preuve de Birkhoff, en français, et deux articles de ce dernier (» réf.4) sur le problème restreint des trois corps (deux d'entre eux ont des orbites circulaires, le troisième, dont on étudie la trajectoire, est de masse négligeable).
|
Théorie des systèmes dynamiques, théorie ergodique : |
Le problème des trois corps est un des problèmes à l'origine de la théorie mathématique des systèmes dynamiques consistant à étudier, en fonction du temps le comportement d'un système régi par des équations mathématiques (système différentiel). Le mathématicien français Jean-Christophe Yoccoz obtint la médaille Fields en 1994 pour les résultats de ses recherches en ce domaine.
En sciences physiques (et en résumant beaucoup), l'ergodicité, introduite par le physicien autrichien Ludwig Boltzmann en 1871, peut s'énoncer comme la propriété, pour un système mécanique donné, de converger en probabilité vers un état final indépendant de son état initial.
Fortet et la notion d'ergodicité : » Yoccoz et la théorie des systèmes dynamiques : »
Théorème ergodique de Birkhoff :
Le théorème ergodique de Birkhoff (1931) est une confirmation mathématique abstraite de l'hypothèse ergodique sous certaines conditions. Concernant ce résultat très difficile, on peut donner la formulation suivante empruntée à l'Encyclopédie Universalis dont l'article sur le sujet (Théorie ergodique, ch. 8), fortement résumé ici, est remarquablement exposé :
Soit Ω
un espace topologique compact muni d'une mesure de Radon m et q une transformation m-mesurable de Ω (l'image réciproque de toute partie mesurable de Ω est mesurable) conservant la mesure (l'image réciproque de toute partie mesurable A de Ω a même mesure que A). Dans ces conditions, soit f : Ω→C une fonction complexe m-intégrable, alors la suite de terme général :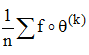
où θ(k) désigne θ o θ o ... θ (k composés) avec θ(o) = idΩ, converge presque partout vers une fonction g μ-intégrable vérifiant g o θ = g et, pour toute partie A μ-mesurable de Ω telle que θ-1(A) = A on a :
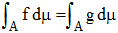
De plus, si les seuls ensembles invariants, outre Ω et Ø, sont les ensembles négligeables (de mesure nulle), alors les fonctions invariantes sont les fonctions constantes presque partout et on a alors presque partout :
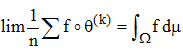
C'est dire que le système abstrait (Ω,θ) vérifie l'hypothèse ergodique. A noter que peu de temps auparavant, Von Neumann énonçait un théorème similaire en se plaçant dans des espaces de Hilbert pour des fonctions de carré intégrable.
➔ Pour en savoir plus :