
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Cet officier d'artillerie, polytechnicien, élève de Monge, fut nommé professeur à l'École d’artillerie de la garde royale (1818) après avoir participé à la guerre d'Espagne. Il se distingua dans l'étude des Surfaces courbes du second ordre (1808) où il exhibe l'hexagone portant son nom et sur la théorie des transversales : géométrie projective. C'est à Brianchon que l'on doit l'expression cercle des neuf points et une démonstration élégante de son existence (1820).
Cercle des neuf points ou cercle d'Euler, également dit de Feuerbach : »
| Hexagone de Brianchon : |
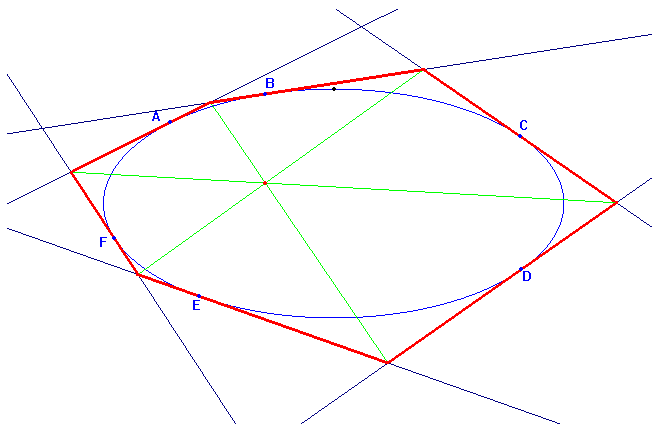
Si l'on considère six tangentes (distinctes) à une
conique, constituant ainsi un hexagone circonscrit à la conique,
alors les trois
diagonales reliant deux sommets opposés sont concourantes
:
La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Vous
pouvez déplacer les points de contact A, B, C, ..., F)
Ce résultat de Brianchon est à l'origine de la recherche sur la dualité en géométrie projective, que rénova Poncelet : il est en effet le dual du théorème de Pascal appelé parfois l'hexagone mystique :
Théorème de Pascal : »