ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Somme de trois carrés
programme JavaScript
»
somme de deux carrés |
somme de 4 carrés (ou moins...)s |
En théorie additive des nombres, la conjecture de Waring, démontrée par Lagrange en 1770 :
Tout entier naturel est la somme d'au plus quatre carrés (éventuellement égaux)
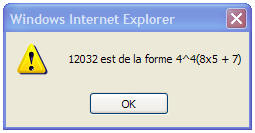
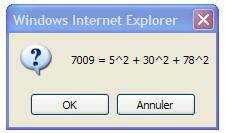
fut complétée par Legendre puis Gauss qui donna une condition nécessaire et suffisante pour qu'un nombre se décompose en trois carrés : il ne doit pas être de la forme 4n(8m + 7), produit d'une puissance de 4 et d'un entier dont le reste dans la division par 8 est égal à 7 (congru à 7 modulo 8). La décomposition n'est pas toujours unique. Par exemple :
62 = 22 + 32 + 72 = 12 + 52 + 62
Il est facile de se convaincre de ces résultats au moyen d'un petit programme élémentaire sur ordinateur. Le programme JavaScript ci-dessous n'est pas optimisé : il trouve des combinaisons redondantes et ne fait appel à aucune étude mathématique du problème : l'ordinateur cherche naïvement. C'est une application de la notion de boucles imbriquées (3 boucles for).
| <SCRIPT
LANGUAGE=JavaScript> function go() { var nbr="",t=0,r=0;p=-1;ok=0 nbr=eval(prompt("Entrez un nombre:",nbr)) if(nbr%4==0) { ns4=nbr while(r==0){r=ns4%4;ns4=ns4/4;p++} ns4=4*ns4;nm7=ns4-7 if(nm7%8==0) { d=nm7/8;r=ns4-8*d alert(nbr+" est de la forme 4^"+p+"(8x"+d+" + "+r+")") // à rejeter selon Gauss if (!confirm("Je le teste quand même ?")) return } } rac=Math.sqrt(nbr) for(i=1;i<=rac;i++) { for(j=i;j<=rac;j++) { for(k=1;k<=rac;k++) { if (nbr==i*i+j*j+k*k) { ok=1 if (!confirm(nbr+" = "+ i +"^2 + "+ j +"^2 + "+ k +"^2")) return } // fin if nbr }}} // fin boucles k, j, i if(ok==0){alert(nbr+" n'est pas décomposable en 3 carrés.")} } </SCRIPT> |
