ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Fonctions sécante et cosécante (d'un angle ou de sa mesure)            » sinus , cosinus ,  tangente , cotangente , sinus & cosinus hyperboliques , tangente & cotangente hyperboliques , exercices

Les fonctions sécante (sec) et cosécante (cosec ou csc) ont été initiées par Abu l'Wafa. Leurs appellations sont dues à Frénicle de Bessy et les notations actuelles à Oughtred.

I - Fonction sécante     

• Nom de la fonction : sécante, abrégé en sec : sec(x) = 1/cos(x). C'est une fonction transcendante.
• Ensemble de définition : R - {π/2 + kπ, k∈Z}
• Périodique : oui, période : 2π.     » la notion de période
• Fonction paire = sec(-x) = sec(x).
• Fonction dérivée : sin(x)/cos²(x) = sin(x)/[1 - sin²(x)].
• Primitive : » exercice :  primitive de 1/cos(x).

sec(x) = cosec (π/2 - x)

• Développement en série :  » Euler | Autres développements :  développements limités usuels

II - Fonction cosécante     

• Nom de la fonction : cosécante, abrégé en cosec ou csc : cosec(x) = 1/sin(x).
  C'est une fonction transcendante.
• Ensemble de définition : R - {kπ, k∈Z}
• Périodique : oui, période : 2π.     » la notion de période
• Fonction impaire = cosec(-x) = - cosec(x).
• Fonction dérivée : - cos(x)/sin²(x) = - cos(x)[1 - cos²(x)].
• Primitive : » exercice :  primitive de 1/sin(x).

cosec(x) = sec (π/2 - x)

• Développement en série :  » Euler | Autres développements :  développements limités usuel

Sécante et cosécante hyperbolique :  »

Dans un repère orthonormé (O,I,J) orienté usuellement par le sens trigonométrique, considérons l'angle ^IOM de mesure x. On a cos x = OH et sin x = OK. La droite (NL) est la tangente en M, perpendiculaire à (OM).

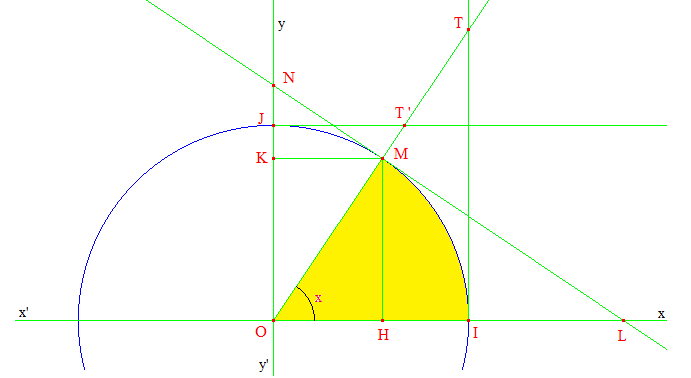
Le triangle MOL est rectangle en M. Dans un triangle rectangle le carré d'un côté de l'angle droit est égal au produit de l'hypoténuse par sa projection sur cette dernière : OM² = OH.OL = OH.OL. On en déduit : OL = 1/cos(x) = sec(x)

Un raisonnement semblable dans le triangle rectangle OMN conduit à ON = 1/sin(x) = cosec(x).

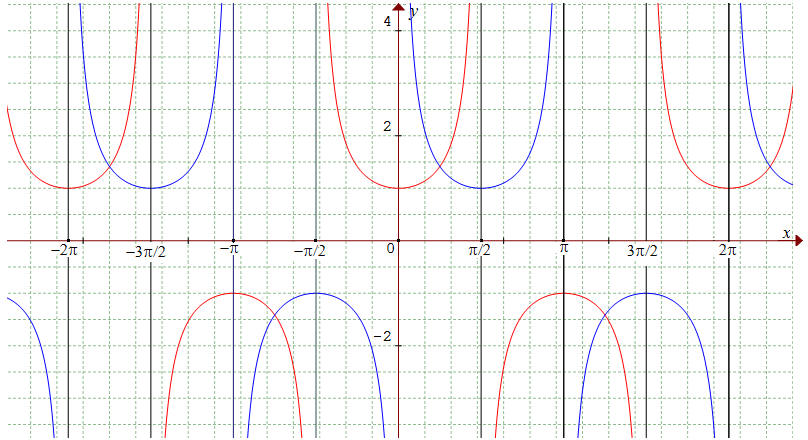
Applications :     

C'est dans la marine et en astronomie que ces fonctions eurent le plus d'intérêt eu égard à la présence récurrente de 1/cos et 1/sin dans les calculs d'angles et de distances comme la parallaxe. Abu l'Wafa en fit grand usage. William Jones dressa des tables très précises de cette fonction sécante.

A titre d'exercice, on vérifiera ces quelques formules :

• sec²x - tan²x = 1               
• csc²x - cotan²x = 1
• sec²x + csc²x = sec²x.csc²x = 1/sec²x.csc²x
• sec(ix) = sech x               
• csc(ix) = -i.csch x      »  sécante et cosécante hyperbolique