
ChronoMath,
une chronologie des MATHÉMATIQUES
à l'usage des professeurs de
mathématiques, des étudiants et des élèves des lycées & collèges

ChronoMath,
une chronologie des MATHÉMATIQUES
à l'usage des professeurs de
mathématiques, des étudiants et des élèves des lycées & collèges
Une excellente approximation de la distance Terre-Lune fut établie en 1751 par les astronomes français Joseph Jérôme Le François de Lalande (1732-1807) et l'abbé Nicolas Louis de La Caille (1713-1762) par une méthode de triangulation calculant la parallaxe de la Lune, c'est à dire l'angle p d'où l'on verrait, depuis le point L de la Lune, un rayon terrestre TA ci-dessous, l'observateur étant en A. On doit à Friedrich W. Bessel le premier calcul de la parallaxe d'une étoile de notre Galaxie : l'étoile 61 du Cygne.
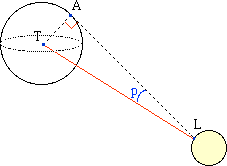
La parallaxe est dite horizontale si l'astre visé est à l'horizon de l'observateur : [LA) est perpendiculaire à [TA]; la parallaxe est alors maximale. La Terre étant aplatie aux pôles (rayon = 6357 km), plus large à l'équateur (rayon = 6378 km) : son "rayon" n'est pas constant.
Par convention, on ramène les calculs à une parallaxe horizontale et pour un rayon équatorial : on parle de parallaxe horizontale équatoriale. On évite ainsi les erreurs (de parallaxe...) liées à des observations faites en des points différents de notre planète. On a ainsi : sin p = AT/TL, et comme p est petit : p ≅ R/TL.
Eu égard à sa petitesse, la mesure directe d'une parallaxe n'est pas envisageable : elle serait entachée de grosses erreurs. Pour la Lune, proche de la Terre, donc de parallaxe relativement grande, on peut procéder à de nombreuses observations et établir une moyenne : ce calcul fut effectué par les astronomes grecs de l'Antiquité (comme Aristarque, Eratosthène, Hipparque, Ptolémée) conduisant à un remarquable résultat de 60 rayons terrestres pour la distance Terre-Lune, distance évaluée aujourd'hui à 60,27 rayons équatoriaux.
➔ Le parsec est une unité de mesure astronomique, terme contracté de parallaxe-seconde : il correspond à la distance d'où l'on voit le rayon moyen de l'orbite terrestre assimilée à un cercle, appelé unité astronomique (UA) sous un angle de 1 seconde d'arc. Cette définition fournit 1 parsec ≅ 3,2616 années-lumière (1 année-lumière est la distance parcourue par la lumière en 1 an à raison de 300 000 km/s) soit 1 parsec ≅ 3,0856 x 1013 km ou 206265 UA.
| Distance Terre-Lune par triangulation : |
 La
parallaxe est un angle très petit : de Lalande se plaça
à Berlin et de La Caille au Cap (Le Cap, Afrique du Sud, lieux situés (pratiquement) sur le même méridien (même
longitude).
La
parallaxe est un angle très petit : de Lalande se plaça
à Berlin et de La Caille au Cap (Le Cap, Afrique du Sud, lieux situés (pratiquement) sur le même méridien (même
longitude).
Ils calculèrent p = 57' 11" (57 minutes et 11 secondes), ce qui est excellent : aujourd'hui, on l'estime à 57' 2" et un réflecteur Laser placé par la NASA (National Aeronautics and Space Administration, U.S.A.) à la surface de la Lune permet de mesurer la distance Terre-Lune à chaque instant et à quelques centimètres près. Distance moyenne : 384 000 km.
i La parallaxe du Soleil est de 8",8 (ce qui fournit une distance d'environ 149 500 000 km).
Étudions comment calculer par triangulation la parallaxe horizontale de la Lune L en fonction de la parallaxe à un instant donné (parallaxe de hauteur), suite à la mesure en un point O de la Terre de la distance zénithale z = ^LOZ de la Lune L (angle par rapport à la direction du zénith de l'observateur O). La figure ci-dessous (n° 87, page 376 verso) et les calculs (pages 358 et 372) sont extraits de l'Astronomie de l'astronome de Lalande, tome 2, présente sur Google Livres (e-book gratuit).
On suppose la Terre sphérique et la trajectoire de la Lune circulaire. L'angle ^OLT = p' est la parallaxe de hauteur. L'angle ^THO = p est la parallaxe horizontale, observée lorsque la Lune est en H, soit lorsque ^HOT = 90°. L'angle h = ^HOL est la hauteur apparente de la Lune pour l'observateur O, dont l'horizon est [OH).
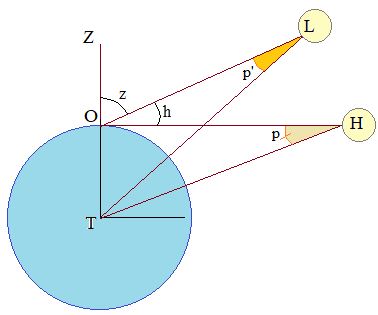

Dans le triangle OTH, on a : OT = HTsin p et dans le triangle OTL, la formule des sinus conduit à :
OT/sin p' = TL/sin^LOT
Mais TL = HT et sin^LOT = sin^LOZ = sin z. Le rapport HT/OT peut donc s'écrire de deux façons : HT/OT = 1/sin p = sin z /sinp', ce que de Lalande exprime ci-dessus (le sinus total signifiant sa valeur maximale, à savoir 1). Et, comme le dit fort justement ci-dessous le célèbre astronome, on peut ici assimiler p et p' à leur sinus, d'où :
p' = p × sin z = p × cos h.

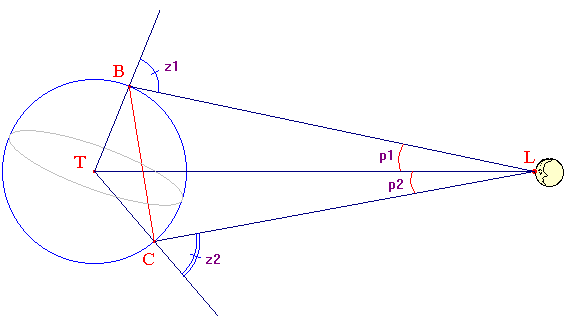
Si maintenant, comme le firent de Lalande et de La Caille, on mesure les distances zénithales z1 et z2 en deux points éloignés d'un même méridien de part et d'autre de l'équateur, afin d'obtenir deux parallaxes p1 et p2, on aura :
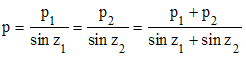 (1)
(1)
➔ Choisir deux points B et C étant éloignés augmente p1 + p2, donc la précision; et le fait de se placer de part et d'autre de l'équateur évite de procéder à une différence des parallaxes, ce qui nuirait encore gravement à la précision des calculs : on se reportera aux erreurs d'arrondi dans le cas d'une différence de deux nombres proches entachés d'erreur.
Les latitudes de B et C sont Φ1 (nord) et Φ2 (sud) : J. de Lalande et N. de La Caille utilisèrent les observatoires de Berlin (Allemagne : 52° 30' N, 13°25' E) et du Cap de Bonne Espérance (Afrique du Sud : 34° 21' S, 18° 28' E) en négligeant les 5° de différence de longitude.
Dans le quadrilatère BTCL, on a ^BTC = Φ1 + Φ2 , donc :
p1 + p2 = 2π - [(π - z1) + (π - z2) + (Φ1 + Φ2)] = z1 + z2 - (Φ1 + Φ2) (2)
D'où la valeur de p au moyen de (1) et (2) ci-dessus. Compte tenu de la petitesse de p1 + p2 et des erreurs d'observation inévitables sur z1, z2, Φ1 et Φ2, cette formule théorique est inexploitable sans recours à plusieurs relevés, lors du passage de la Lune au méridien d'observation, afin d'en tirer une moyenne.
De plus, les mesures de chaque observateur doivent être simultanées et à l'époque point d'horloge atomique ! il fallait se fier aux distances de la Lune par rapport à des étoiles considérées comme fixes vu leur éloignement. La Caille fit un grand nombre de mesures ultérieures (une quarantaine) à Paris, Greenwich, Stockholm, Bologne.

La formule des sinus fournit maintenant TB/TL = sin^TLB/sin^TBL et TC/TL = sin^TLC/sin^LCD. D'où :
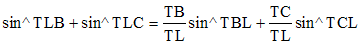
En assimilant p1 et p2, exprimés en radians, à leur sinus et en conservant les rayons terrestres effectifs TB et TC en B et C, on a, comme le conclut de Lalande (page 374 de son traité) :
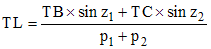
Ces formules conduisent à environ 380 000 km (à l'époque : 85 490 lieues), un très bon résultat que discute de Lalande en tenant compte de l'aplatissement des pôles (Terre plus elliptique que sphérique) et des résultats de ses confrères, comme Mayer.