
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» étude analytique de la podaire d'un cercle |
|
Soit (c) un cercle de centre A, de rayon a. O un point extérieur à ce cercle, M un point courant du cercle. La perpendiculaire issue de O à la tangente en M à (c) coupe cette dernière en P. Il s'agit de trouver le lieu de P, tracé ci-dessous en rose.
Traçons le cercle (c') de diamètre [OA]. Il coupe (OP) en Q.
On suppose M extérieur de
(c').
Montrer que PQ = AM, donc que si on pose OQ = r, alors OP =
r + a
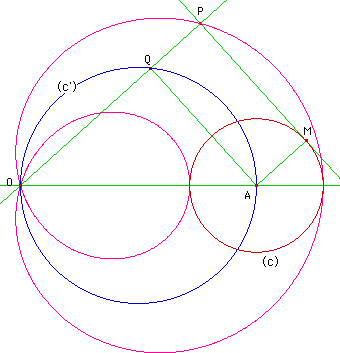
On suppose M à l'intérieur de (c'). Montrer que PQ = AM, donc que OP = r - a
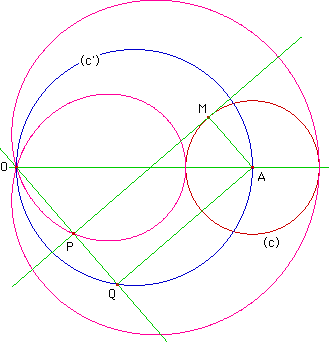
En faisant usage des coordonnées polaires (r,t) de pôle O :
Montrer que si l'on pose d = OA, alors r = dcost est une équation polaire du cercle (c')
Montrer que P décrit un limaçon de Pascal (conchoïde de cercle) et que si O est choisi sur (c), ce limaçon se réduit à une cardioïde.
La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :
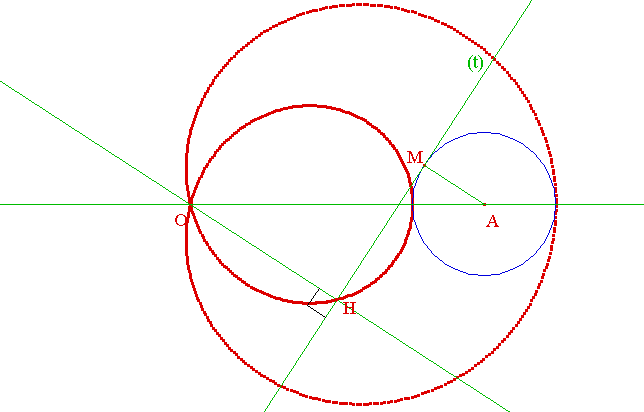
![]()
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Vous pouvez agrandir/réduire le cercle de
centre A et déplacer A et O.
Vous pouvez effacer / relancer le
lieu :
double-cliquer /
cliquer
dans la figure
Vous pouvez aussi déplacer M manuellement.