ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Podaire d'un cercle   Étude analytique          »  étude géométrique

Soit (c) un cercle de centre A, de rayon r. O un point extérieur à ce cercle, M un point courant du cercle. La perpendiculaire issue de O à la tangente en M à (c) coupe cette dernière en H. Il s'agit de trouver le lieu de H, tracé ci-dessous en rose.

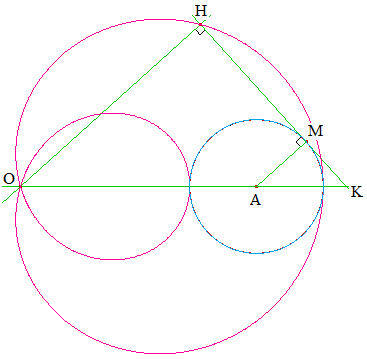
Choisissons O comme origine des coordonnées. On pose a = OA et t = ^(OA,OH). On peut procéder de deux façons :

• Les droites (PH) et (AM) sont parallèles. Soit K l'intersection de (PA) et (HM). Par usage du théorème de Thalès, montrer que OH = r + acost. En déduire que H décrit la courbe d'équation x = cost(r + acost) , y = sint(r + acost).

ou bien :

• On utilise l'équation générale de la podaire d'une courbe par rapport à l'origine :

x et y désignent les coordonnées du point courant de (c), à savoir : x = a + rcos t , y = rsin t. Le calcul conduit à la même équation que ci-dessus.

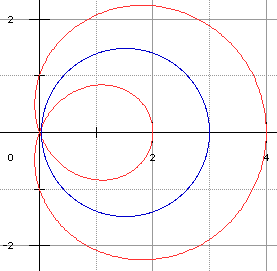
 ➔  On retrouve bien là l'équation d'une conchoïde de cercle : celle du cercle de diamètre [OA]. En effet l'équation polaire de ce cercle est ρ = acost. La conchoïde (pour le module r) a alors pour équation polaire :