ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Conchoïde d'une courbe               » Trisection selon Nicomède

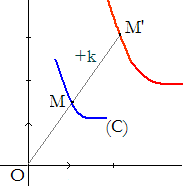
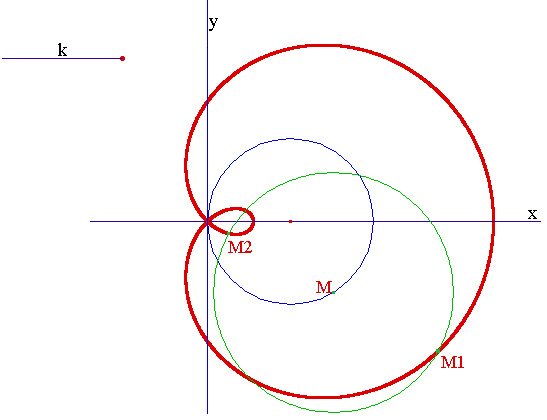
Une conchoïde d'une courbe (C) relativement à (ou par rapport à) un point O et à un nombre positif k est obtenue, lorsque M décrit (C), comme le lieu des points M' alignés avec O et M et tels que MM' = k. Deux point M1 et M2 symétriques par rapport à M répondent donc généralement à la question.

» Conchoïde est forgé sur concha = coquillage (latin) et eïdos = forme (grec), signifiant donc en forme de coquillage. Une étymologie certes indiscutable mais peu convaincante eu égard à la forme des courbes étudiées ici...

Si r = f(t) est l'équation polaire de la courbe (C), le rayon-vecteur est r = OM. L'équation de la conchoïde relativement à l'origine O est alors :

r = f(t) ± k

Les conchoïdes ont des formes diverses suivant le support de la courbe utilisé. On s'intéresse ici aux conchoïdes de cercles et aux conchoïdes de droites :

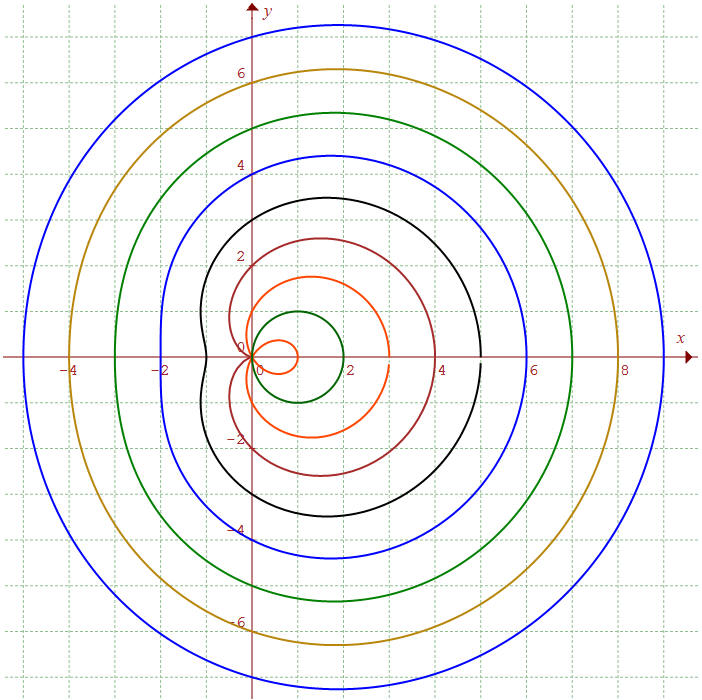
L'équation polaire d'un cercle de centre A(a/2,0) de diamètre a est r = a.cost, par suite les courbes d'équation de la forme :

r = a.cost + k

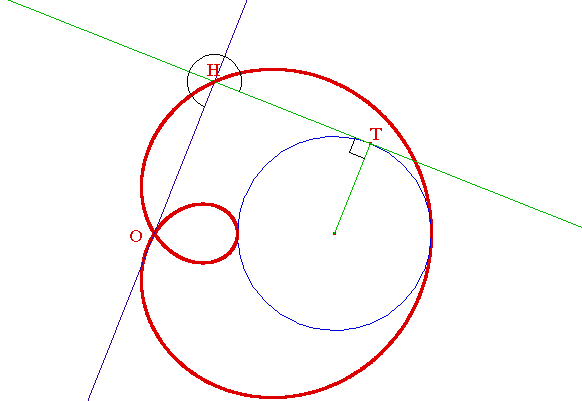
sont des conchoïdes de cercle relativement à l'origine, également appelés limaçons de Pascal, du nom d'Etienne Pascal, père de Blaise, qui les a étudiées en tant qu'ensemble des pieds H des perpendiculaires abaissées d’un point fixe O sur les tangentes à un cercle : podaire d'un cercle.

Animations :  »

• Conchoïde d'équation r = 2cost + k, k ∈{0, 1, 2, ..., 7}. Le cas k = 0 correspond au cercle (en vert). La conchoïde à boucle (en rouge correspond à k = 1 (a > k).

• La conchoïde en forme de cœur, cardioïde, cas particulier se produisant lorsque k = a. Son équation est ici : r = 2cost + 2.
  L'équation r' = 2cost - 2 conduit à la même courbe : en effet r(t + π) = - r'(t).

Cardioïde en tant qu'épicycloïde : »         Cardioïdographe sur YouTube : »

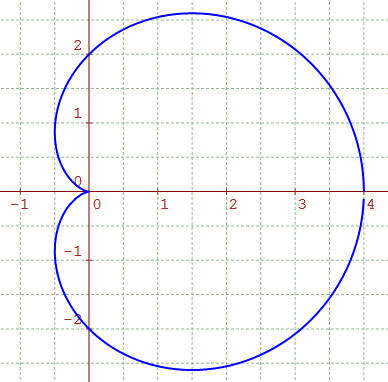
• Une conchoïde avec boucle. Cela se produit lorsque a > 1. Son équation est ici : r = 4cost + 2. Les tangentes à l'origine (point double) on pour équation y = ± x√3. Cette courbe une quartique (courbe algébrique du 4è degré) dont une équation implicite peut s'écrire (x² + y² - 4x)² - 4(x² + y²) = 0. On obtiendra aisément cette équation en utilisant r² = x² + y², x = (4cost + 2)cost  et y =  (4cost + 2)sint. En développant l'équation, les tangentes au point double, ici l'origine, s'obtiennent en annulant les termes de plus bas degré, soit 12x² - 4y² = 0 ou encore y = ± x√3 (» théorème de Cramer).

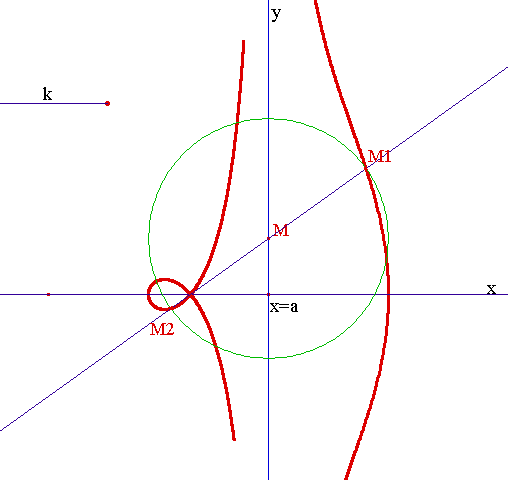
L'équation polaire d'une droite d'équation cartésienne x = a, en repère orthonormé est r = a/cost, par suite les courbes d'équation de la forme r =a/cost + k sont des conchoïdes de droite par rapport à l'origine. Un exemple célèbre est la conchoïde de Nicomède illustrée ci-dessous.

Voici la conchoïde d'une droite d'équation x = a par rapport à O. [M₁M₂] est un diamètre du cercle de centre  M, de rayon k. La conchoïde est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
Vous pouvez déplacer M et changer k en jouant sur la tirette
Pour effacer/relancer le lieu : double-cliquer/cliquer dans la figure

Conchoïdographe sur YouTube :  »