
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
Matrice hessienne et forme quadratique |
f désignant une fonction numérique (à valeurs dans R) définie sur un ouvert U de R2 et au moins deux fois continument dérivable (ses dérivées partielles d'ordre 1 et 2 existent et sont continues sur U), on se place en un point (a,b) où le gradient de f est nul (point critique) :
∂f/∂x1 = ∂f/∂x2 = 0
C'est une condition nécessaire d'extremum :
Formule de Taylor et extremum d'une fonction de plusieurs variables : »
Le problème est alors de connaître le comportement de f au voisinage de ce point (minimum, maximum, point selle). En cas de point critique, le développement de Taylor de la fonction f au voisinage de (a,b) peut s'écrire :
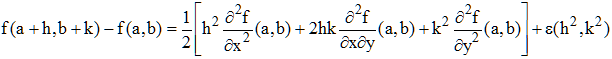
Appelons Δf le 1er membre. On reconnaît dans le crochet une forme quadratique de type
q(h,k) = Ah2 + 2Bhk + Ck2
Si on se place suffisamment proche de (a,b), h et k sont infiniment petits et Δf est du signe de q(h,k).
D'autre part, comme expliqué à la page consacrée à Otto Hesse, ce développement peut s'écrire au moyen de la matrice de Hesse :
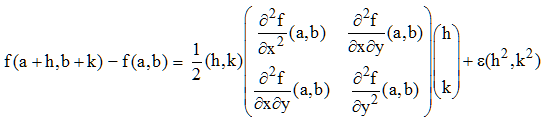
La matrice de Hesse étant symétrique, elle est diagonalisable et le théorème de décomposition de Gauss nous permet d'écrire :
q(h,k) = λ1[L1(h,k)]2 + λ2[L2(h,k)]2
où λ1 et λ2 sont les valeurs propres de Hesse(f) au point (a,b), L1 et L2 étant des formes linéaires du 1er degré en h et k.
Le déterminant DH de la matrice diagonale est λ1λ2 : c'est le déterminant de Hesse, invariant dans ce changement de base.
La trace TH de la matrice hessienne, somme des dérivées partielles secondes par rapport à chaque variable est λ1 + λ2 également invariante dans le changement de base.
Par conséquent, sans qu'il soit nécessaire, dans ce cas, de faire le calcul des valeurs propres de la matrice hessienne :
Si DH > 0 : les valeurs propres sont de même signe :
Si TH > 0 : les valeurs propres sont positives, donc Δf > 0 : au voisinage de (a,b), f prend des valeurs supérieures à f(a,b); c'est dire que f passe par un minimum.
Si TH
< 0 : les valeurs propres sont négatives, donc Δf < 0 : au
voisinage de (a,b), f prend des valeurs inférieures à f(a,b); c'est dire
que f passe par un maximum.
Si DH = 0 : une au moins des deux valeurs propres est nulle. C'est un cas litigieux :
Si λ1 = λ2 = 0, alors q(h,k) = 0. Il faudra alors développer à l'ordre 3 (au moins ) pour connaître le comportement de f au point (a,b) en étudiant le signe de :
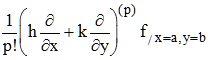
Si une seule des valeurs propres est nulle, alors q(h,k) = 0 est du type
±(αh
+ βk)2. Le signe de la trace TH
permettra de conclure.
Si DH < 0 : les valeurs propres sont de signes contraires :
Suivant les valeurs de h et k, q(h,k) = λ1h2 + λ2k2 prendra également des valeurs de signes contraires au voisinage du point étudié : on est en présence d'un col, à rapprocher des points d'inflexion des fonctions d'une variable et des point hyperboliques au sens des surfaces (point selle). On remarquera la similitude (bien naturelle) avec les résultats obtenus dans l'étude de :
L'indicatrice de Dupin : »
Cette discussion (n = 2) se généralise à n variables par la même voie de réduction de la forme quadratique avec le calcul effectif des valeurs propres de la matrice hessienne :
∗∗∗
Étude locale d'une fonction de 3
variables
Exercice résolu (n = 2) :
On pose f(x,y) = x3 + y4 - yx2 - xy2.
a/ Montrer l'existence de trois points
critiques.
b/ Étudier leurs natures dans le cas x = y.
➔
Pour en savoir
plus :
Cours de mathématiques supérieures, V. Smirnov, Ch. 5 - Éd. Mir - Moscou
Pages de Henri Immediato (Université Lyon 1), exercices :
http://nte-serveur.univ-lyon1.fr/immediato/Math/Enseignement/05 Analyse/29 -
Extrema relatifs...html
Pages de Stéphane Leborgne (université Rennes 1)
» exercice 2 :
http://perso.univ-rennes1.fr/stephane.leborgne/Corrections.pdf