ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Valeurs propres, vecteurs propres         ∗∗∗ exercices d'application      » Polynôme caractéristique | spectre | diagonalisation et triangulation d'une matrice | application aux systèmes différentiels

Cette page suppose connues les notions d'application linéaire, de matrice d'application linéaire et de déterminant :

Soit f une application linéaire, élément de L(E,F) où E et F sont des espaces vectoriels sur un même corps commutatif K. On appelle valeur propre de f, un nombre k de K pour lequel :

On dit alors que V est un vecteur propre de f associé à k.

L'avantage majeur de ces concepts sera la possibilité d'étudier une application linéaire, ou tout autre objet lié à une représentation matricielle, dans une représentation simple grâce à un changement de base sur laquelle la restriction de f est une homothétie. Mais cela n'est pas toujours possible : la nature de K (dans la pratique R ou C) joue un rôle capital.

 ➔   La notation λ (lambda, L minuscule en grec ) est à la valeur propre ce que x est à l'inconnue ! Nous sacrifions donc à cette notation et on se restreint dans toute la suite au cas d'un endomorphisme (F = E).

Voici quelques résultats, conséquences immédiates de la définition que le lecteur (niveau L1) pourra facilement prouver; f désigne un endomorphisme, élément de L(E),

• r0/ f admet la valeur propre λ = 0 si et seulement si f est non bijective : son noyau est distinct de {0}.

• r1/ Si V est un vecteur propre associé à la valeur propre λ non nulle de f, la droite vectorielle D engendrée par V est globalement invariante par f : f(D) = D. Autrement dit, la restriction de f à D est une homothétie vectorielle de rapport λ.
   !  La droite vectorielle D ne sera invariante vecteur par vecteur que si λ = 1.

• r2/ On peut aussi exprimer r1 en disant que tout vecteur non nul colinéaire à un vecteur propre V est un vecteur propre associé à la même valeur propre de f : c'est dire que tout vecteur propre engendre une droite vectorielle, sous-espace vectoriel de dimension 1.

∗∗∗
f et g désignant deux endomorphismes, montrer que toute valeur propre non nulle de f o g est aussi valeur propre de g o f. Rép. : ici

• r3/ Si λ est une valeur propre de f, alors λⁿ est une valeur propre de f ⁿ = f o f... o f o f;

Voici deux théorèmes fondamentaux dont les démonstrations sont (encore) laissées au lecteur :

Théorème 1 :     

λ est une valeur propre de f si et seulement si l'endomorphisme f - λ.id_E est non injectif,

Autrement dit, au moyen du noyau d'un endomorphisme, noté Ker :

λ est une valeur propre de f si et seulement si Ker(f - λ.id_E) est non réduit à {0_E}

On voit donc que si K = R, un endomorphisme peut ne posséder aucune valeur propre. Par contre si K = C, tout polynôme admet au moins un zéro et, par suite, f admet au moins une valeur propre réelle ou complexe. Si M désigne une matrice carrée, le déterminant de la matrice M - λI, où I désigne la matrice unité, s'appelle encore le polynôme caractéristique de M

Théorème de Cayley-Hamilton : »

Spectre d'un endomorphisme :   

L'ensemble des valeurs propres de f (resp. d'une matrice M) est le spectre de f (resp. de M). Un des usages fondamentaux des valeurs et vecteurs propres se rencontre dans la réduction des équations des formes quadratiques.

Diagonalisation d'une matrice, triangulation : »

 ➔  En dimension infinie et dans le cas plus général d'espaces vectoriels normés un complexe λ tel que f - λid_E ne soit pas inversible est appelé valeur spectrale. La théorie spectrale est une importante branche de l'analyse fonctionnelle qui s'est développée, en particulier avec Fredholm, Riesz et Sturm, autour de l'étude des solutions des équations intégrales.

Application à la résolution d'un système différentiel linéaire : »

1. Soit f  l'endomorphisme de E dont la matrice dans une base B = (i,j) est :

• i/  Montrer que f n'admet pas de valeurs propres M;
• ii/ On suppose que C remplace R en tant que corps de scalaires, Montrer que f admet les valeurs propres complexes i et - i et que les droites vectorielles engendrées par les vecteurs propres associés ont pour équation : x + y(1 ± i) = 0.

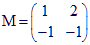
2. E est ici de dimension 3 sur R; B = (i,j,k) est une base de E; f est l'endomorphisme dont la matrice relativement à B est :

• En vérifiant que le polynôme caractéristique de f admet λ = 1 comme zéro, montrer qu'il existe une base de E dans laquelle la matrice de f est de la forme diagonale :

 
 

---

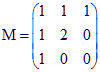
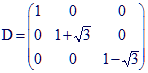
3. E est un espace vectoriel quelconque (réel ou complexe).

• On suppose que f o f = f (projecteur) : montrer que les valeurs propres de f sont 0 ou 1.
• On suppose que f o f = id_E (symétrie) : montrer que les valeurs propres de f sont 1 ou -1.
• On suppose que E est euclidien (espace vectoriel normé) et que f est une isométrie; montrer que les valeurs propres de f ne peuvent être que - 1 et 1.

4. Donner une interprétation géométrique des endomorphismes de l'espace dont les matrices respectives sont :

 
 

---

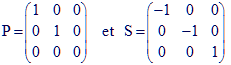
 ➔   Pour en savoir plus :

• Tout cours niveau universitaire L2,  MP/MPSI 1ère et 2è année.

• Valeurs propres sur Université en ligne :
  http://uel.unisciel.fr/physique/outils_nancy/outils_nancy_ch11/co/apprendre_ch11_20.html

• Matrix Calculator (dont valeurs et vecteurs propres : https://matrixcalc.org/fr/vectors.html

• Systèmes différentiels sur le site Université en ligne :
  http://uel.unisciel.fr/mathematiques/sys_diff/sys_diff_ch02/co/apprendre_ch2_01.html (et ch2_02, ch2_03)