ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 Convergence
spirale (ou
en escargot) d'une
suite récurrente
» Autres cas : divergence "spirale" , convergence en "escalier" , usage d'une suite auxiliaire |
➔ Cet exercice est une application de l'inégalité des accroissements finis : » Lagrange.
On considère la suite numérique (u) définie, pour tout n de N, par la relation de récurrence :
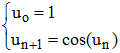
1°/ Tracer la courbe représentative de f : x → cos x sur l'intervalle [0;1] dans un repère orthonormé d'unité 10 cm. Tracer la droite δ d'équation y = x.
On a :
u1 = cos uo = cos 1; on reporte cette valeur sur δ; on en déduit :
u2 = cos u1; on reporte cette valeur sur δ; on en déduit :
u3 = cos u2; on reporte cette valeur sur δ; on en déduit :
...
un+1 = cos un;
...
Programme JavaScript de contrôle de convergence d'une suite un = f(un-1): »
➔ On constate une "rapide" convergence en spirale, également dite en escargot, vers un point d'abscisse a, compris entre 0,7 et 0,8 et vérifiant tant y = a (point de δ) que y = cos a (point de la courbe), soit :
cos
a = a
On justifiera facilement que pour toute suite (u) convergente, de limite L, définie par une relation du type un+1 = f(un), f désignant une fonction continue, on a nécessairement f(L) = L.
Construction d'un cas convergent où f est non continue : »
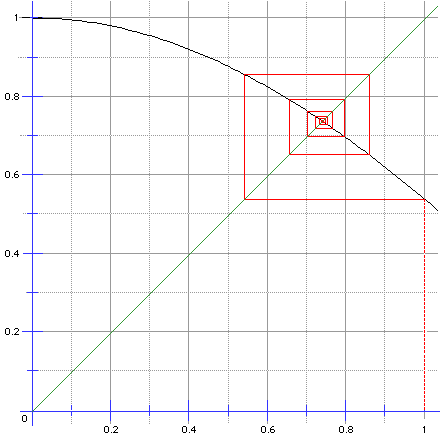
Cette convergence en spirale exprime une oscillation des valeurs prises par la suite autour de a (alternativement supérieures et inférieures). Cela est dû au fait que la fonction cosinus est décroissante :
un < un-1 ⇒ f(un) > f(un-1) ⇒ un+1 > un
un+1 > un ⇒ f(un+1) < f(un) ⇒ un+2 < un+1
etc.
On est en droit de conjecturer que la suite (un) est convergente vers a. Prouvons-le :
2°/ Vérifier
par récurrence que pour tout n de N, on a 0 < un <
1.
3°/ On
pose k = sin 1; montrer, en utilisant l'inégalité des
accroissements finis, que pour tout couple (x,y) de [0;1], on a :
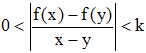
4°/ Vérifier par récurrence que pour tout n de N, on a :
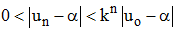
En remarquant que 0 < k < 1, prouver la convergence de la suite (un) vers a.
5°/ Il est facile d'obtenir, par encadrements successifs, une valeur approchée assez précise de a :
a @ 0,739085
On peut procéder par dichotomie ou par pas décimaux (programmes JavaScript) :
Méthode des pas décimaux : » Théorèmes de points fixes : »