ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Suite du type un+1 = f(un) et continuité de f           niveau Sup       » Convergence "spirale" , Divergence "spirale" , convergence en "escalier" , usage d'une suite auxiliaire

L'objectif est ici de montrer qu'une suite définie par une récurrence du type v_n+1 = g(v_n) peut converger vers une limite L ne vérifiant pas nécessairement g(L) = L lorsque g n'est pas continue.

Soit f une fonction numérique continue sur R et (u) la suite numérique non stationnaire définie par la relation de récurrence u_n+1 = f(u_n), u_o donné. On suppose que la suite (u) est convergente; on note L sa limite. Par continuité de f, on a f(L) = L. On trouvera en lien ci-dessous le cas d'une telle suite :

Étude de la suite u_n+1 = cos(u_n) :  ››››

I - On note U l'ensemble des valeurs de la suite (u) lorsque n décrit N.

1°/ Justifier que U est un ensemble borné de R.

2°/ Justifier que L∉U.

II - On pose :

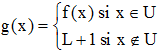
et soit (v) la suite définie par v_o = u_o et v_n+1 = g(v_n).

3°/ Justifier que g n'est pas continue au point L.

    » On remarquera d'ailleurs que g étant constante presque partout (car U est dénombrable), g est
         discontinue presque partout.

4°/ Justifier (par récurrence) que la suite (v) coïncide en fait avec la suite (u) et converge donc vers L mais que l'on n'a cependant pas g(L) = L.

Théorèmes de points fixes :  ››››