ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
|
|
Voici un premier exemple simple d'application d'un important théorème sur les suites monotones bornées définies par une récurrence de la forme un+1 = f(un). La simplicité de l'étude est due à la croissance de la fonction f, laquelle implique, suivant la valeur de u0 , la croissance ou la décroissance de la suite.
On considère la suite numérique définie, pour tout n de N, par la relation de récurrence :
uo = [-1;1] et, pour tout n de N* : 2u2n+1 = 1 + un
1°/ On pose :
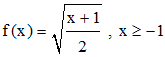
Vérifier que la fonction f est strictement croissante. On trace sa courbe représentative (c) ainsi que la droite (d) d'équation y = x.
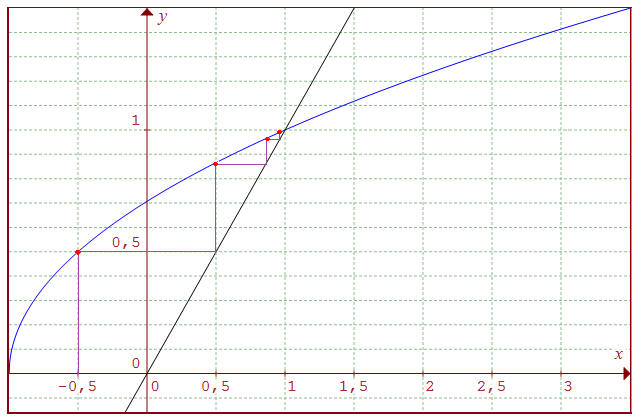
On a choisi
ci-dessous uo = -1/2 :
u1 = f(uo) = f(-1/2) = √(1/4) = 1/2; on reporte cette valeur sur (d); on en déduit :
u2 = f(u1) = f(√3/2) ≅ 0.9659; on reporte cette valeur sur (d); on en déduit :
u3 = f(u2) ≅ 0.9914; on reporte cette valeur sur (d); on en déduit :
...
un+1 = f(un);
...
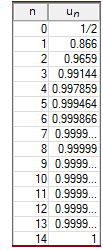
Programme JavaScript de contrôle de convergence d'une suite un = f(un-1): »
On constate une "rapide" convergence (croissante) en escalier vers un point d'abscisse a situé sur (d), vérifiant ainsi :
f(a) = a
➔ Au vu du graphique obtenu, il semble donc que la suite soit strictement décroissante et converge vers a = 1. La valeur est un point fixe de f.
Prouvons-le :
2°/ Vérifier par récurrence que pour tout n de N*, on a 0 < un < 1.
3°/ Montrer que la suite (un) est strictement croissante (utiliser la stricte croissance de f).
4°/ Déduire de 2° et 3° que la suite (un) est convergente vers un réel a tel que f(a) = a et que a = 1.
5°/ Étudier les cas u0 = -1 et u0 = 1.
Théorèmes de points fixes : »
Convergence en escalier d'une
suite récurrente du type un+1 = f(un) #1