
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 » Cas du deltoïde | Cas de l'astroïde | Épicycloïde | Autres cas |
 |
Rappelons que la développée d'une courbe (C) est la courbe enveloppe des normales de (C). En bleu, ci-dessous, est tracée la néphroïde d'équation :

Sa développée, générée par ses normales, que l'on peut observer en blanc au centre de l'image, est aussi une néphroïde dont l'équation peut ici s'écrire :
Eu égard aux formules cos3t = 4cos3t - 3cos t et sin3t = 3sin t - 4sin3t, on peut remarquer que x = 2cos3t mais que l'écriture de y ne se simplifie pas. La recherche de cette équation est relativement simple si l'on se réfère à la page consacrée à l'équation générale de la développée d'une courbe :
On a ici :
X = x - n2y'/d et Y = y + n2x'/d;
d = x'y" - x"y' = 36(1 - cos2t);
n2 = x'2 + y'2 = 18(1 - cos2t).
On a donc n2/d = 1/2, ce qui nous conduit facilement à X = x - y'/2 = (3cos t + cos3t)/2 et Y = y + x'/2 = (3sin t + sin3t)/2.
On peut conjecturer graphiquement qu'il existe entre la néphroïde et sa développée une transformation géométrique simple : rotation d'angle π/2 sans doute suivie d'une homothétie de rapport 1/2. Pour vérifier cela, il suffit, de s'assurer que la courbe d'équation
X = 3cos t + cos3t et Y = 3sin t + sin3t
est l'image de notre néphroïde par rotation d'angle pi/2.
L'expression analytique d'une rotation de centre O, d'angle π/2, est donnée par la relation matricielle :
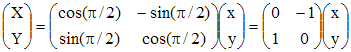
C'est dire que X = -y et Y = x. Ce qui fournit X = -3sin t + sin3t et Y = 3cos t - cos3t. Nous pouvons effectuer le changement de variable t = T - π/2 :
Y = 3cos
C'est bien l'équation recherchée.
Génération de la courbe :
La développée est générée ci-dessous au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Pour
effacer / relancer le lieu
double-cliquer /
cliquer
dans la figure
»
Outils CabriJava