ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
Développée de l'astroïde        » Astroïde | Autres développées dans ChronoMath

L'astroïde s'obtient comme lieu d'un point M d'un cercle de rayon r roulant sans glisser à l'intérieur d'un cercle de rayon R = 4r. Son équation, lorsque r = 1 est alors :

x = 3cos t + cos 3t , y = 3sin t - sin 3t

Les résultats concernant l'étude générale de la développée d'une courbe plane, fournissent l'équation de sa développée :

X = x - n2y'/d  et  Y = y + n2x'/d ,   d = x'y" - x"y' et n2 = x'2 + y'2

avec d = x'y" - x"y' et n2 = x'2 + y'2. Un petit et patient calcul montre que d = -n2 = 18(cos 4t - 1). Donc X = x + y' et Y = y - x', soit :

X = 6cos t - 2cos 3t , Y = 6sin t + 2sin 3t

Et voici l'astroïde (en rouge) et sa développée (en bleu) vues par Graphmatica :

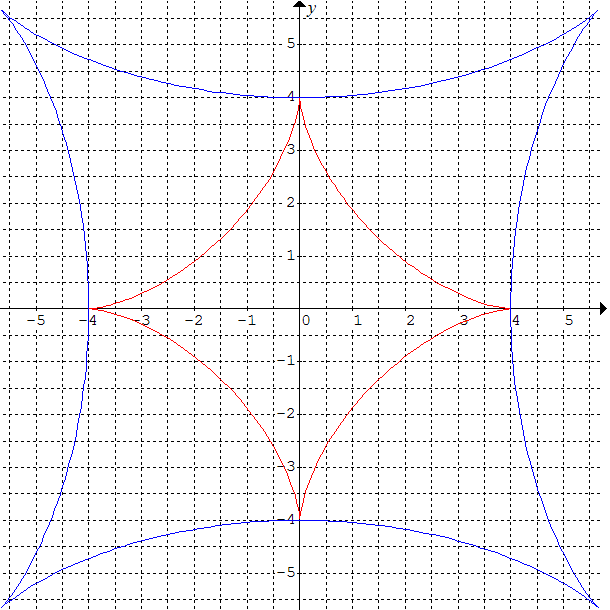
La courbe est manifestement une astroïde obtenue par similitude de centre O, de rapport 2, d'angle π/4. Vérifions cela. Nous avons :

X = 6cos t - 2cos 3t = 2(3cos t - cos 3t), Y = 6sin t + 2sin 3t = 2(3sin t + sin 3t)

L'homothétie semble manifestement de rapport 2. Si nous montrons que la courbe d'équation X = 3cos t - cos 3t, Y = 3sin t + sin 3t est l'image de notre astroïde par rotation de π/4, c'est gagné. L'expression analytique d'une rotation de centre O, d'angle π/4, est donnée par la relation matricielle :

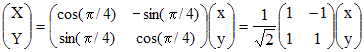
C'est dire que X = (x - y)/√2  et Y = (x + y)/√2. Calculons alors x - y et x + y lorsque x et y désignent les coordonnées d'un point de notre astroïde :

  • x - y = 3cost + cos3t - 3sint + sin3t = 3(cost - sint) + cos3t + sin3t
            = 3[cost - cos(π/2 - t)] + cos3t + cos(π/2 - 3t)

  • On applique les formules de transformations de sommes en produits, conduisant à  X = -3sin(t - π/4) + cos(3t - π/4).

Après avoir posé t - π/4 = T - π/2, c'est à dire t = T - π/4, on obtient : X = 3cosT - cos3T.

  • x + y = 3cost + cos3t + 3sint - sin3t = 3(cost + sint) + cos3t - sin3t
            = 3[cost + cos(π/2 - t)] + cos3t - cos(π/2 - 3t)

Un calcul semblable à celui de X conduit  sans difficultés à Y = 3sinT + sin3T.

Génération de la développée de l'astroïde :   

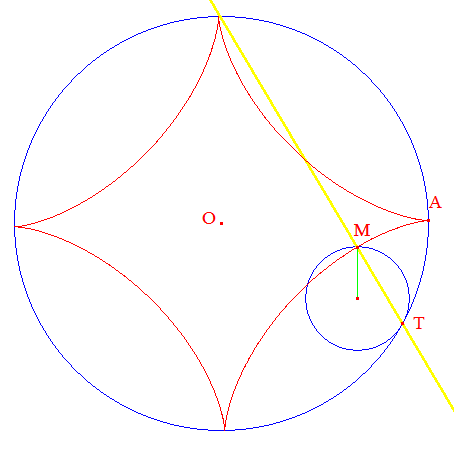
La développée est générée ci-dessous au moyen d'un logiciel de géométrie dynamique, ici Cabri Géomètre, dans sa version CabriJava pour Internet :



 Si votre navigateur accepte les applets Java (» extension CheerpJ) :
T peut être déplacé. La normale en M est (TM) de couleur jaune. Pour effacer/relancer le lieu double-cliquer.

Autres développées et développantes dans ChronoMath : »

© Serge Mehl - www.chronomath.com