
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 |
|

➔ Variantes :
Si tu sèches après avoir bien cherché : ››››
| Solution à compléter : |
Enoncé : On considère un rectangle ABCD. On note J et K les milieux respectifs des côtés [AB] et [CD].
Question : Que peut-on dire du point d'intersection de la diagonale [AC] avec le segment [JK] ?
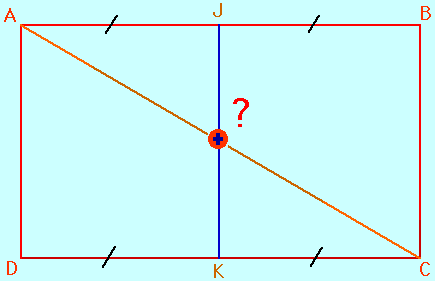
Réponse à la question (à compléter...) :
Le quadrilatère ABCD étant un ............., il admet un .......... de .............. O qui est le ............. commun de ses ................ [.......] et [BD].
Appelons S la symétrie (centrale) de centre O.
J est le ............ de [AB]
et on sait que la symétrie centrale conserve les
milieux.
Or l'image de [AB] par S est [C....]. L'image de J par
S est donc le point K, milieu de [.....].
[JK] et [AC] ont donc le même milieu : le centre de la symétrie S c'est à dire O, centre du rectangle.
➔ Variantes :
En 5ème et 4ème
: l'usage des
symétries, c'est bien beau mais fait penser à
pourquoi faire simple quand on peut faire
compliqué...
tracer [AK] et [JC]. Le quadrilatère AJCK
est un parallélogramme. Pourquoi ? conclure.
En 3ème : la propriété de Thalès dans sa configuration "croisée" conduit à :