ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 |
Apprendre à construire, apprendre à rédiger :
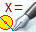symétrie centrale #2niveau 5è/4è » cours , #1 , #3 |
- Trace un carré ABCD; appelle O son centre;
» c'est dire que O est le point d'intersection des diagonales- Place le symétrique E de C par rapport à B;
- Place le symétrique F de B par rapport à A;
- Place le symétrique G de A par rapport à D;
- Place le symétrique H de D par rapport à C.
Vérifier la figure et continuer l'exercice : ››››
Symétrie centrale #2
(suite) niveau
5è/4è
»
Rappel de cours
»
#1 ,
#3 |
Voici la figure que tu dois obtenir :
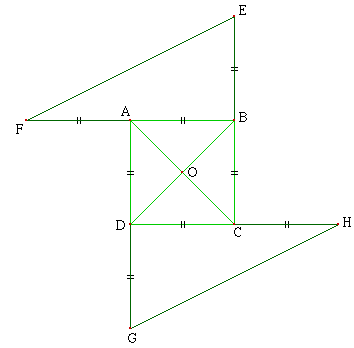
C'est bon ? Prouve maintenant que les triangles DGH et EFB sont symétriques par rapport à O.
Ce qui revient à dire que :
le symétrique du triangle GHD par la symétrie de centre O est le triangle EFB
ou encore :
l'image du triangle DGH par la symétrie de centre O est le triangle EFB
| Solution à compléter : |
a/ ABCD étant un carré de centre O, on peut déjà affirmer que D est le ................. de B dans la symétrie de centre O.
b/ Traçons les segments [FD] et [BH].
Par la symétrie de centre A, les points B, A et F sont ................. et AB = .........
Par la symétrie de centre C, les points D, C et H sont ................. et ........ = .........
Or, ABCD étant un carré, on a (BF) // (......). Le quadrilatère FDHB ayant deux côtés ...................... et de même ................ est un ...................................... et ses diagonales se coupent donc en leur ............. : c'est donc le point O.
J'en déduis que H est l'image de ...... dans la symétrie de centre O.
c/ Traçons maintenant les segments [AE] et [GC].
Par un raisonnement semblable au précédent, je déduis que le quadrilatère AECG est un parallélogramme de centre ...... et que ........ est l'image de ...... dans la symétrie de centre O.
Finalement, dans la symétrie de centre O : E → G, F → H, B → D, l'image du triangle EFB est le triangle GHD.
