ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 |
 Un problème d'invariant...
TD niveau 4ème/3ème
» variante symétrie axiale niveau seconde |
Voici un triangle isocèle ABC de sommet principal A. On a tracé la hauteur issue de C. Le point M est mobile sur [BC].
On demande de prouver que la somme des
distances MK + ML du point M aux côtés
[AB] et [AC] ne dépend pas de la position
de M.
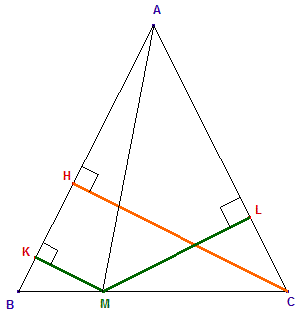
La même figure générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ
) :
On
peut déplacer le point M et modifier les dimensions du triangle ABC en déplaçant
A, B ou C.
Indications :
♦ Traçer [AM].
♦ On sait que l'aire d'un triangle est le demi-produit de la mesure d'un côté par la hauteur relative à ce côté.
♦ Quelle est l'aire du triangle ABM ?
♦ Quelle est l'aire du triangle ACM ?
♦ Expliquer pourquoi la somme de ces aires est celle de ABC, c'est à dire la moitié de AB x CH.
♦ En déduire CH = MK + ML et ce qu'il fallait démontrer...