ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
  Parallélogramme
& bissectrices #1 »
#2
niveau
5è/4è |
On considère un parallélogramme ABCD.
Les bissectrices des angles ^A et ^B se
coupent en E.
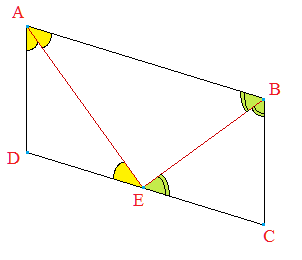
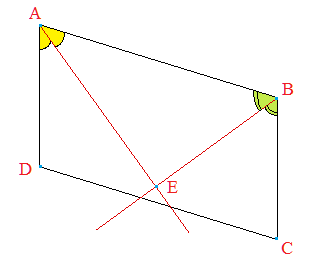
En général, E n'est pas situé sur
[DC] comme le montre la figure ci-dessous.
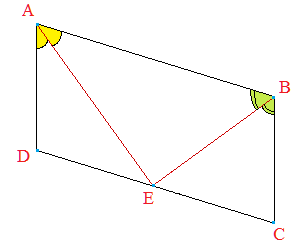
Nous allons supposer dans ce problème que E est situé sur [DC] :
Comparer les mesures des côtés [AB] et [BC]
➔ Prolongements :
Étudier la réciproque.
Etudier le rapport AB/BC suivant la position de E à l'intérieur, sur, et à l'extérieur du parallélogramme.
Si tu sèches après avoir bien cherché (solution à compléter) : ››››
| Solution : |
Supposons E sur [CD].
ABCD étant un ........................., les droites (AB) et (.....) sont parallèles et coupées par la sécante (AE). Par conséquent, les angles alternes-internes ^BAE et ^.......... sont égaux (même mesure).
[AE) étant la bissectrice de l'angle ^DAB, on a ^DAE = ^........... En conséquence, le triangle DAE est isocèle en ........ Par suite AD = DE
En raisonnant de la même façon sur l'angle ^ABC, on en déduirait que le triangle ........... est isocèle en C. Donc BC = .........
Mais AD = BC. D'où E est le ................ de [DC] et la relation cherchée est AB = 2BC
On pourra énoncer et prouver la réciproque de cette jolie propriété
