ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Trapèze & bissectrices     TD niveau 5ème        »   trapèze & segment médian , trapèze & diagonales , trapèze isocèle

• On considère un trapèze ABCD, de bases (côtés parallèles) [AB] et [CD].
• Les bissectrices des angles de ce trapèze déterminent un quadrilatère IJKL :

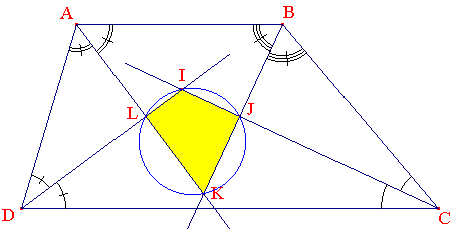
On constate que ce quadrilatère est inscriptible : I, J, K et L sont cocycliques (sur un même cercle).

Pourquoi ?

Indications :  

• Prouver tout d'abord que les angles ^BAD et ^ADC d'une part, ^ABC et ^BCD d'autre part sont supplémentaires en tant qu'angles correspondants dans une situation à préciser...

• Trace [IK]; remarquer que les triangles KLI et KJI semblent rectangles...
• Prouve cette conjecture en évaluant les angles ^ALD et ^BJC...

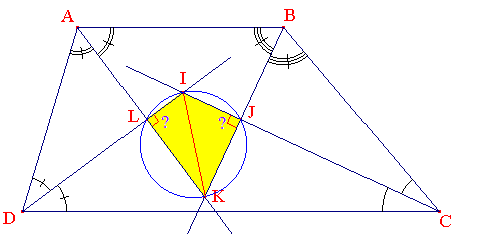
☼ Et souviens-toi que :

Tout triangle rectangle s'inscrit dans un cercle dont le diamètre est son hypoténuse

Prolongement : 

Que devient ce résultat lorsque le trapèze est un parallélogramme : [AD] et [BC] également parallèles ? 

Parallélogramme et bissectrices : ››››