
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
On note un = 2n/(2n - 1)k le terme général de la série donnée, à savoir :
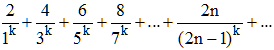
1°/ Lorsque k = 1, le terme général est supérieur à 1. Il ne tend donc pas vers 0 : la série est divergente.
2°/ Lorsque k = 2, le terme général peut s'écrire :
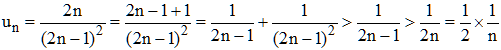
La série de terme général vn = 1/n est divergente : série harmonique. La série donnée diverge donc a fortiori.
3°/ Considérons maintenant la série de terme général wn = 1/(2n)k-1. On vérifie alors que le rapport un/wn tend vers 1. Les deux séries sont donc de même nature.
Critères de convergence des séries numériques : ››››
On peut écrire :
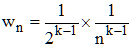
On voit là le terme général de la série de référence 1/nα qui converge si et seulement si α = k - 1 > 1. Notre série est donc convergente si et seulement si k > 2.