ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Étude d'une série #4  calcul de π par intégration d'un développement en série et programme JavaScript     »  version tableur | calcul selon Gregory en #3      » #1 ,  #2 , #3 ,  #5 , #6

Si (u_n) est une suite géométrique de raison r, | r | < 1, de premier terme 1, on sait que la somme S_n = 1 + r + r² + ... r^n-1 de ses n premiers termes a pour limite le nombre :

Par suite, pour tout x de l'intervalle ouvert ]-1,+1[, nous pouvons écrire, avec r = -x² :

(s)      

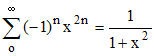
En posant f_n(x) = (-1)ⁿx²ⁿ, la série de fonctions ci-dessus converge normalement sur tout intervalle [0,a] inclus dans [0,1[. En effet, pour tout x de l'intervalle [0,a], on a : | f_n(x) | = x²ⁿ  < a²ⁿ et ce dernier nombre est le terme général d'une série géométrique convergente puisque 0 < a² < 1.

Par ailleurs, f : x →tan(x) réalise une bijection de [0,π/4[ sur [0,1[. La fonction g = f^-1 : x →atan(x) réalise donc une bijection dérivable de [0,1[ sur [0,π/4[ et l'on a :

La convergence étant normale, on peut déduire par intégration terme à terme :

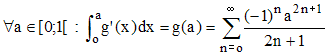
On a en particulier, lorsque a = 1/√3, g(1/√3) = π/6, et on en déduit :

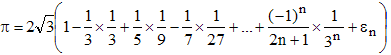
La formule obtenue est facilement programmable et converge assez rapidement mais pour nous en assurer nous devons majorer le reste ε_n. Notons(Σ) la série de terme général :

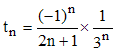
(Σ) est manifestement alternée, strictement décroissante et à termes positifs. Il suit, selon un résultat de Leibniz, que |ε_n| est strictement inférieur à | t_n+1 |.

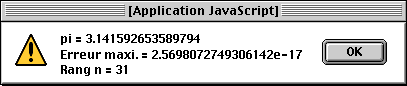
L'inégalité |ε_n| < | t_n+1 | est fondamentale car non seulement elle prouve la convergence du procédé mais elle permet aussi d'évaluer l'erreur commise sur la somme de la série en s'arrêtant au rang n. Le défaut dans ce type de calcul est évident : on ajoute à une somme de type S_n-1, un terme t_n tendant vers 0. On ne s'étonnera pas qu'à partir d'un certain rang, nous aurons S_n = S_n-1 car le terme | t_n | décroissant vers 0 deviendra nul pour la machine ! Le résultat obtenu est remarquable à 10 ^-16 près au rang n = 31.