ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Triangle et aire #2
niveau 4ème/3ème
»
#1 (niveau 5ème/4ème) |
 |
La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :
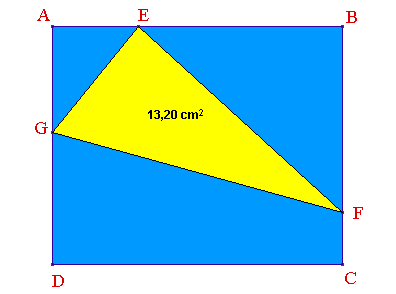
On considère un rectangle ABCD. Les points E, F et G peuvant se déplacer sur les côtés [AB], [BC] et [AD], ce qui change alors l'aire du triangle EFG.
Si ton navigateur accepte les applets
Java :
Tu peux déplacer les points E, F
et G.
Pour la question 1, ne modifie pas le rectangle.
Question 1:
Où situer E, F et G afin que l'aire du triangle EFG soit maximale ?
Indication :
On tracera la parallèle à (AD) passant par E.
Question 2 (prolongement) :
En déplaçant A, B ou D : on obtient le cas plus général où ABCD est un parallélogramme. Vérifier que la réponse donnée dans le cas du rectangle reste valable.
| Solution : |
Traçons la parallèle à (AD) passant par E; elle coupe [FG] en L.
Soit H le pied de la hauteur issue de G dans le triangle EGL et K le pied de la hauteur issue de F dans le triangle EFL.
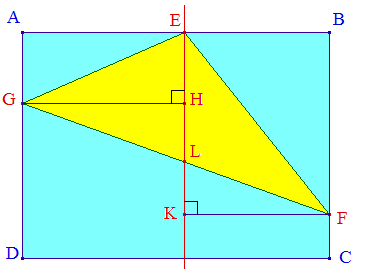
L'aire du triangle EFG est :
EL x GH/2 + EL x FK/2 = EL x CD/2
L'aire est donc maximale lorsque EL est maximale, donc lorsque L est sur [DC].
Mais cela ne se peut que si G est en D et F en C, le point E étant quelconque sur [AB].
Prolongement :
Si ABCD est un parallélogramme; le même raisonnement s'applique :
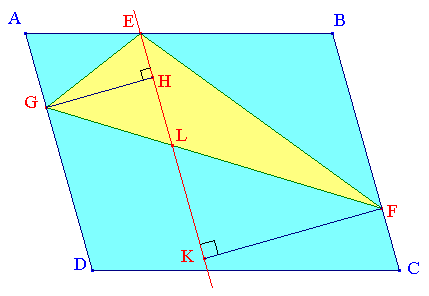
Cette fois, l'aire du triangle EFG est :
EL × (GH + KF)/2
Les droites (AD), (EL) et (BC) étant parallèles, (GH) est perpendiculaire à (AD) et (KF) est perpendiculaire à (BC).
GF + KF est donc la distance entre les côtés (AD) et (BC) du parallélogramme ABCD : c'est un nombre invariant lorsque E, F et G se déplacent (tout comme précédemment).
La conclusion est donc la même.