ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Étude d'un endomorphisme de l'espace (diagonalisation)    niveau Sup           outil : déterminant d'ordre 3

E est de dimension 3 sur R. B = (i,j,k) est une base de E et f l'endomorphisme de E dont l'expression analytique, relativement à B est :

1°/ Écrire la matrice M de f. vous devriez trouver :

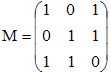
 Montrer, en calculant le déterminant de f, que cet endomorphisme est bijectif.

2°/ Montrer que l'ensemble des vecteurs invariants par f est une droite vectorielle dont on précisera un vecteur directeur u.

3°/ Montrer que l'ensemble des vecteurs changés en leur opposé par f est une droite vectorielle dont on précisera un
vecteur directeur v.

4°/ Montrer que l'ensemble des vecteurs z tels que f(z) = 2z par f est une droite vectorielle dont on précisera un vecteur directeur w.

5°/ Montrer que (u,v,w) est une base de E et exprimer la matrice M' de f dans cette base; Vérifier par le calcul que det(M) = det(M').

Éléments de réponse :   

• Le déterminant de f est celui de sa matrice M, soit det(f) = det(M) = -2.
• Par rapport à la base B, on trouvera facilement : u(1,-1,0) ; v(1,1,-2) ; w(1,1,1)
• B' = (u,v,w) est une base de E car son déterminant est det_B(B') = 6 ≠ 0.
• f(u) = u ; f(v) = -v et f(w) = 2w.
• La matrice de f dans la base (u,v,w) est l'écriture en colonne de f(u), f(v), f(w). Par conséquent :

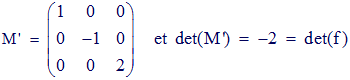
 ➔  Dans la base B', la matrice M est donc diagonale.