ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
Une intégrale pas vraiment simple...
niveau Sup» voir aussi : Exemples d'intégration par parties | Intégrales diverses | primitives de 1/sin x et 1/cos x | primitives de e1/x |
On se propose de calculer l'intégrale ci-dessous au moyen d'une décomposition en éléments simples. On trouvera sur le site une seconde méthode de calcul plus subtile sur la page consacrée au théorème des résidus, ainsi qu'une troisième faisant usage des intégrales eulériennes de 1ère espèce.
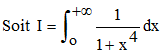
1°) On vérifiera tout d'abord les identités :
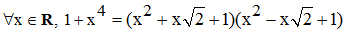
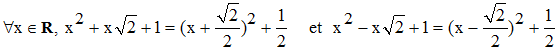
2°) Les facteurs x2 ± x√2 + 1 n'admettent pas de racines réelles. La décomposition en éléments simples de 1/(1 + x4) s'écrit alors sous la forme :
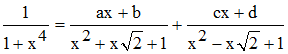
En procédant par identification, on montrera facilement que a = - c = √2/4, b = d = 1/2, puis que :
3°) Soit ε = ±1 et y > 0. On peut écrire :
Calculons Jε par le changement de variable t = x + ε√2/2. Il, vient en remplaçant :
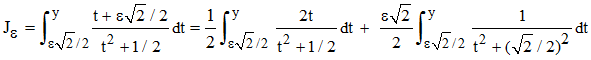
L'intégrande de la première intégrale du second membre est du type φ'(t)/φ(t), de primitive ln |φ(t)| + C; l'intégrande de la seconde est du type 1/(t2 + a2), avec a = √2/2, de primitive 1/a × atn(t/a) + C, atn désignant la fonction arc tangente, fonction réciproque de tan. Par suite :
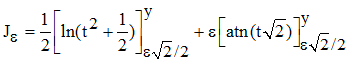
Dans le logarithme t est au carré, par conséquent, dans le calcul de la différence J1 - J-1, les logarithmes pour la borne y s'éliminent. Quant à la borne ε√2/2, elle conduit à t2 + 1/2 = 1 : les logarithmes pour cette borne sont donc nuls. Il nous reste alors seulement :
J1 - J-1 = 2 × atn(y√2) - atn(1) - atn(-1).
Lorsque y tend vers + ∞, il en est de même de y√2, donc atn(y√2) tend π/2; d'autre part atn(1) = π/4 et atn(-1) = -π/4. Donc :
J1 - J-1 = π - π/4 + π/4 = π et I = π√2/4.