
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
La fonction x→e1/x est continue sur ]-∞,0[∪]0,+∞[ = R*, elle admet donc des primitives (ne différant que d'une constante additive C). Mais, tout comme, par exemple la fonction x→ 1/x, pour laquelle les mathématiciens ont inventé la fonction logarithme, elles ne sont pas calculables au moyen des outils élémentaires de l'analyse. Il nous faut recourir au développement en série de puissances de x.
Nous voulons donc calculer :
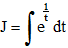
Posons x = -1/t. On a dx = x2du. L'intégrale J devient :
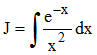
Intégrons par parties en constatant que 1/x2 est la dérivée de -1/x. On obtient sans difficultés :

Le calcul élémentaire s'arrête là... On sait que la fonction exponentielle de base e est développable en série entière ex = ∑xn/n!et que ce développement converge uniformément pour tout x de R. Dans ces conditions :
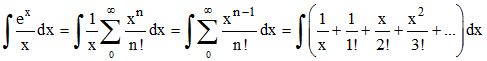
Et finalement, la convergence uniforme permettant d'intégrer terme à terme :
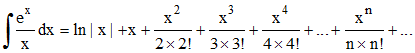
D'où :
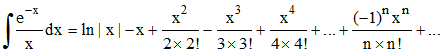
Revenons à J : -e-x/x peut s'écrire -∑ (-1)nxn-1/n! = - 1/x + 1 - x/2! + x2/3! - x3/4!...
En conclusion :
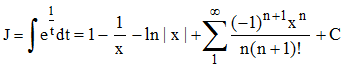
Quelques primitives et intégrales classiques : ››››