ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Abonnement
(solution)
fonctions linéaires et affines
niveau 3è/2nde |
1°/
Le coût du tarif normal est donné
par la fonction linéaire
f : x → 0,9x.
Le coût de l'abonnement est donné
par la fonction affine
g : x → 0,5x + 12.
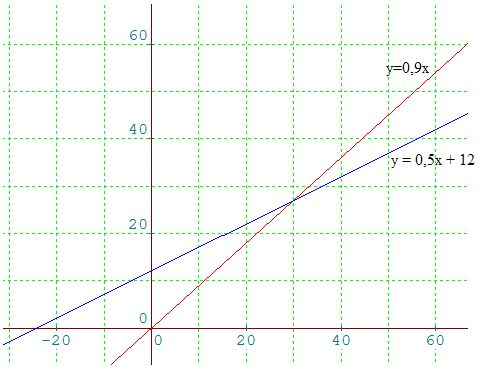
2°/ On trace alors les droites d'équation :
y = 0,9x (en rouge) et y = 0,5x + 12 (en bleu)
On lit sur le graphique qu'à partir de x = 30, le coût du tarif normal (en rouge) devient supérieur au coût de l'abonnement (en bleu).
3°/ Dire que le coût de l'abonnement est plus intéressant que le tarif normal c'est chercher à résoudre l'inéquation g(x) < f(x), soit à résoudre :
0,5x + 12 < 0,9x
|
On a successivement : 0,5x - 0,9x < -12 x > 30 |
On retrouve bien qu'au delà de x = 30, le coût de l'abonnement est moindre que le tarif normal. |
4°/ Une année comprend 52 semaines; l'économie est donc f(52) - g(52), soit 8,8 euros.
On peut tenter de lire
la réponse sur
le graphique à condition que celui-ci soit précis (papier millimétré) mais au
risque d'une solution approchée : on constate que pour x = 52, l'ordonnée de f (droite rouge) correspond à 46,8 et l'ordonnée de g (droite bleu) correspond à 38 : la différence est 8,8.