
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

» Variantes : Tubes en pyramide , Pyramide de disques |

On a placé 3 boules de même diamètre 30 cm et tangentes deux à deux.
Par dessus a été placée une quatrième boule identique.
Quelle est la hauteur exacte de la "pyramide" ainsi obtenue ?
| Solution |
Les 4 boules étant tangentes deux à deux, les centres A, B C et S de ces boules forment un tétraèdre régulier SABC comme indiqué ci-dessous (les faces sont des triangles équilatéraux de côté 2r). Si r est le diamètre des boules, et h la hauteur du tétraèdre, la hauteur cherchée de la pyramide est h + 2R.
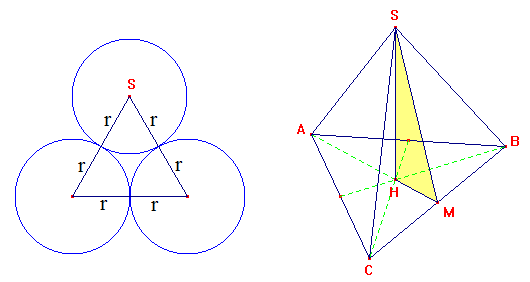
Par raison de symétrie, le sommet s se projette à égale distance de A, B et C, donc au point de concours des médiatrices, qui est aussi le centre de gravité du triangle équilatéral ABC. Donc HM = AM/3 et AM, hauteur dans ABC, mesure 2r√3/2 = r√3.
Ainsi : HM = (r√3)/3 = r/√3. Pour le calcul de SH, on applique le théorème de Pythagore dans le triangle rectangle SHM avec SM = AM = r√3 : SH2 = SM2 - HM2.
On trouve alors SH2 = 8r2/3. Par suite SH = 2r√2/√3. En conclusion, la hauteur est donnée par la formule :
![]()
Numériquement, eu égard au diamètre indiqué 2r = 30 cm , la hauteur est 54,5 cm à 1 mm près.