Milne William Edwin

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

MILNE William Edwin, américain, 1890-1971

! On ne confondra pas William Milne avec l'astrophysicien anglais Edward Arthur Milne (1896-1950), spécialiste en mécanique relativiste qui fut professeur de mathématiques à Oxford.

Diplômé de Harvard en 1915, Milne fut professeur à l'université d'Oregon dont il dirigea le département mathématique de 1932 à sa retraite en 1955. Il fut un des pionniers en analyse numérique en s'intéressant très tôt aux possibilités offertes par l'informatique dans la résolution numérique des équations différentielles.

Correction (ou méthode) de Milne pour l'intégration approchée (également dite de Boole-Villarceau) :

Il s'agit d'une extrapolation de Richardson adaptée à la méthode de Simpson pour 3 et 5 points. Soit à calculer une approximation J de l'intégrale :

Pour 3 points x_o = a, x₂ = (a + b)/2 , x₄ = b, on a h = (b - a)/2 et

J₃ = (y_o+ 4y₂ + y₄) × h/3 , y_i= f(x_i) (j3)

Pour 5 points : x_o = a, x₁ = a + h/2, x₂ = (a + b)/2, x₃ = x₂ + h/2, x₄ = b et :

J₅ = (y_o+ 4y₁ + 2y₂+ 4y₃ + y₄) × h/6 , y_i= f(x_i) (j5)

Partant de la méthode des trapèzes, on sait que la méthode de Simpson apparaît comme le résultat de l'extrapolation de Richardson pour 2 et 4 points. L'extrapolation J de J3 et J5 fournit donc au rang suivant :

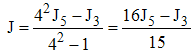
Et un petit calcul fournit l'approximation de Milne pour 5 points que l'on peut généraliser à n points, lorsque n est multiple de 5 :

➔ On pourra remarquer que la méthode de Milne équivaut à la méthode de Newton-Cotes pour une interpolation de degré 4. Elle est donc exacte pour des polynômes de d° ≤ 5.

Programmation de la méthode en JavaScript

Pour tester ce programme vous devez entrer votre fonction en utilisant une syntaxe comprise par le langage JavaScript. L'instruction with (Math), placée en début de procédure, évite à l'utilisateur de préciser Math devant chaque fonction mathématique utilisée. Les opérations et fonctions usuelles sont les suivantes :

multiplication : * , division : /
racine carrée : sqrt(x)
puissance : pow(x,n). Pour x² ou x³, utiliser plutôt x*x et x*x*x
fonctions usuelles : sin(), cos(), tan(), atan(), abs();
log népérien : log() , exponentielle de base e : exp() , ...
les appellations pi (pour π) et e sont comprises par le programme.

» fonctions mathématiques usuelles

<SCRIPT LANGUAGE=JavaScript>
var fonc
var pi=3.141592653589793;
var e=2.7182818284590452;

function meth()
{with (Math)
{
fonc="4/(1+x*x)";a=0 ; b=1 ; n=100;fonc=prompt("Entrez votre fonction :",fonc)
if (fonc==null) {return}
a=eval(prompt("Entrez a :",a));if (a==null) {return}
b=eval(prompt("Entrez b :",b));if (b==null) {return}
n=prompt("Nombre de points voulus = ",n);if (n==null) {return} else {n =eval(n)};
r=n%4;n=ceil(n/4)*4; // n sera un multiple de 4 par excès
if (r!=0){alert("J'ai choisi n = "+n+ " (multiple de 4).")}
h=(b-a)/n;j=0;
for(i=0;i<=n-4;i=i+4){x=a+i*h;j=j+7*f(x)+32*f(x+h)+12*f(x+2*h)+32*f(x+3*h)+7*f(x+4*h)}
alert("Integrale = "+j*h*2/45)
}
}

function f(x)
{
with(Math){y=eval(fonc);return y}
}
</SCRIPT>

Exemple d'exécution :

Par défaut f(x) = 4/(1+x²), a = 1, b = 1, n =100. Le programme fournit donc 4Atn(x) entre 0 et 1 soit 4 x π/4. Le programme calcule donc une approximation de π : 3,141592653589919... :

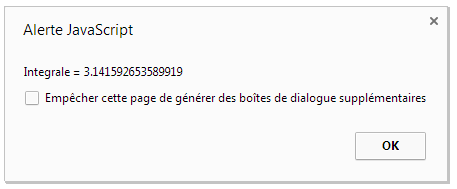
Pas mal ! L'erreur est théoriquement en 1/n⁷.

1000 décimales de π : » Autres méthodes d'intégration approchée : »

➔ Pour en savoir plus :

Compléments biographiques sur le site de l'Oregon State University

Gonseth

Fraenkel