ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
JOACHIMSTHAL
(Joachimstal) Ferdinand,
allemand, 1818-1861 |
» Source éléments biographiques : Deutsche Biographie
Né à Goldberg (ville de Pologne en Silésie, anciennement prussienne), Ferdinand Joachimsthal étudie la philosophie à Berlin où il obtient son doctorat en 1842. Professeur de lycée à Berlin, il poursuit des études de mathématiques et soutient une thèse sur les courbes algébriques (1845). Ce n'est qu'en 1853 qu'une chaire de mathématiques lui sera offerte à l'université de Halle où il rencontra Hesse (en 1855) avec lequel il travailla sur l'introduction de méthodes algébriques en géométrie. Il fut nommé à Breslau en 1856.
Joachimsthal contribua au Journal de Crelle et aux Nouvelles Annales Mathématiques de Gerono et Terquem. On lui doit un certain nombre de résultats originaux sur les coniques :
|
Cercle de Joachimsthal : |
Soit M un point intérieur à l'ellipse dont on peut mener quatre normales. en A, B, C et D. Alors le cercle circonscrit au triangle ABC passe par le point D' diamétralement opposé à D (symétrique de D par rapport au centre de l'ellipse.
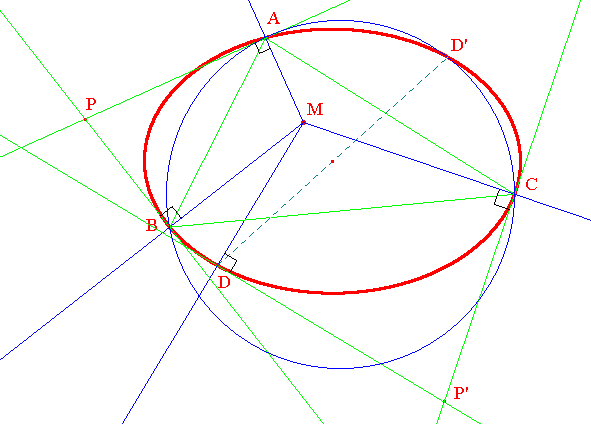
➔ Il n'est pas toujours possible de tracer 4 normales à une ellipse (E) depuis M intérieur à (E). On démontre que deux sont toujours assurées. Lorsque l'ellipse est donnée sous sa forme réduite x2/a2 + y2/b2 = 1, alors si M(α,β), α et β non nuls, les pieds des normales sont solutions du système obtenu en ajoutant l'équation de l'hyperbole (dite d'Apollonius), d'équation :
a2αy - b2αx = c2xy
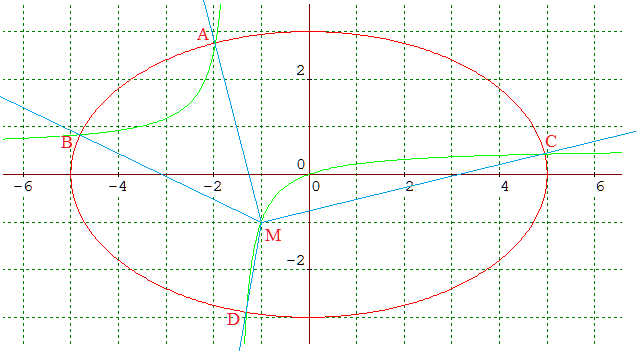
La développée de l'ellipse est l'enveloppe de ses normales. On pourra tracer quatre normales à l'ellipse depuis M à condition que M soit situé à l'intérieur du contour de la développée et en dehors des axes (focal et transverse) :
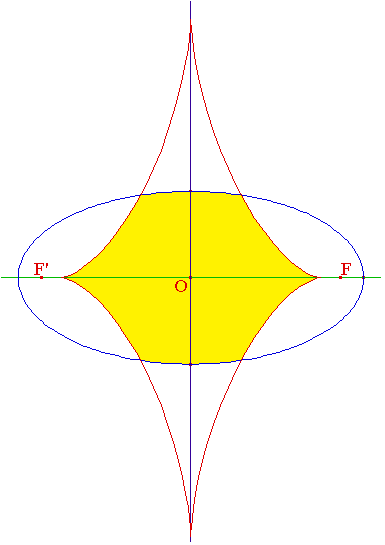
et la condition sur M(α,β) est a2/3α2/3 + b2/3β2/3 < c4/3.
|
Condition de cocyclicité de 4 points d'une ellipse : |
On considère une ellipse paramétrée par x = a.cost, y = b.sint.
Quatre points de l'ellipse définis par les 4 valeurs t1, t1, t1 et t1 du paramètre sont cocycliques si et seulement si t1, t1, t1 et t1 est un multiple de 2π.
Ce beau théorème fait l'objet d'une belle démonstration de Gilles Costantini. Le lien est précisé en réf.4 ci-dessous.
» Poncelet
➔ Pour en savoir plus :
Sur les normales aux coniques par F. Joachimsthal (1870) :
http://archive.numdam.org/article/NAM_1870_2_9__481_0.pdf
Sur quelques théorèmes de Joachimsthal par
Edmond Laguerre :
http://archive.numdam.org/article/BSMF_1877__5__92_1.pdf
Sur les normales aux coniques par
E. Catalan (1848) :
http://archive.numdam.org/article/NAM_1848_1_7__332_1.pdf
Preuve du théorème de cocyclicité (Gilles Costantini) :
files.math6c.webnode.fr/200000006-9dff59ef98/joachimsthal.pdf
Bonnet