
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Autres trisections dans ChronoMath | » Voir l'animation |
 |
Nicomède proposa une solution approchée de la trisection de l'angle (partage d'un angle en trois angles de même mesure) par la construction d'une trisectrice, c'est à dire une courbe permettant une trisection approchée :
^xOA est l'angle que nous voudrions trisecter. Soit K le projeté orthogonal de A sur [Ox) et [Az) la parallèle à [Ox) menée par A. Supposons placé sur [AK] le point B, tel que [OB) coupe [Az) en un point M pour lequel BM = 2OA.
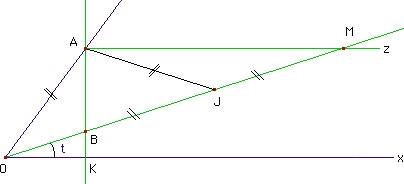
En traçant la médiane issue de A dans le triangle BAM, on voit que ^AOB est le double de l'angle ^BOK. Il apparaît ainsi que :
l'angle ^xOM est le tiers de l'angle donné ^xOA
En effet, vu que BAM est rectangle en A, on a JA = JM = OA. Or ^BOK = ^JMA (alternes-internes). D'où, en notant t la mesure de ^BOK : ^AOB = ^OJA = 2t, c'est dire que ^xOA = 3t.
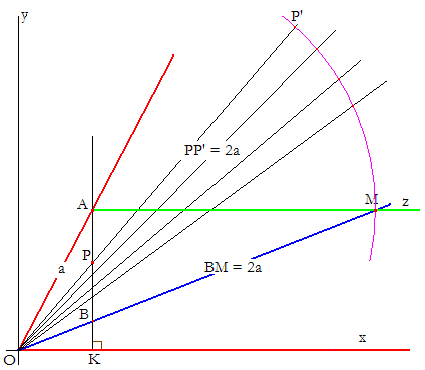
Le problème est donc de déterminer M. Plaçons nous dans un repère orthonormé et posons a = OA.
A tout point P situé sur [AK], on associe le point P' de [OP), tel que OP' = OP + 2a (donc PP' = 2a).
Tracez le plus grand nombre possible de demi-droites [OP) en reportant PP' = 2a.
Vous voyez se construire point par point la branche (Γ) de la trisectrice.
Cette construction étant achevée :
La parallèle à (Ox) passant par A coupe (Γ) en M, réalisant la trisection de l'angle ^xOA
Figure dynamique :
La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :
Choisissez un angle xÔy en déplaçant [Ay);
Déplacer P jusqu'à ce que M soit situé sur [Az). xÔM réalise la trisection de l'angle xÔA.
L'angle xÔy étant choisi, le logiciel trace l'ensemble des points M lorsque P varie.

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Déplacer P comme indiqué ci-dessus. Pour effacer le lieu (ensemble des
points M), double-cliquer dans la figure
» la précision de
la mesure des angles est de l'ordre de 0,1
degré.
En notation moderne, l'équation polaire de la trisectrice ainsi obtenue est
C'est une conchoïde (prononcer conkoïde ) de la droite (AK).
➔ D'une façon générale, une conchoïde d'une courbe (C) relativement à un point O et à un nombre positif k, est obtenue, lorsque M décrit (C), comme le lieu des points M' alignés avec O et M et tels que MM' = k.
En savoir plus sur les conchoïdes, animation : »
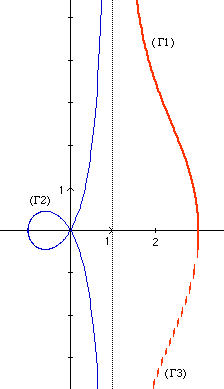 |
Ci-contre, la
conchoïde
(Γ) de la
droite d'équation polaire r = 1/cos t (soit x = 1 en coordonnées cartésiennes). L'équation polaire de la courbe est : r = 1/cos t + 2 Le paramètre t varie de 0 à 2π. Les
portions (Γ1),
(Γ2) et
(Γ3)
correspondent respectivement » Morley |
➔ Pour en savoir plus (constructions diverses et célèbres) :
CES PROBLÈMES QUI FONT LES MATHÉMATIQUES
(la trisection de l'angle), par Jean Aymes - Apmep/Ass.Prof.Math.Ens. (1989)